题目内容
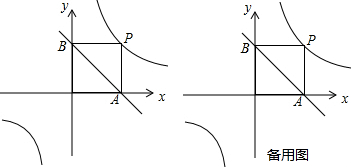
已知直线y=-x+1交x,y轴于A,B两点,反比例函数y=
在第一象限内的图象上有点P,连AP,BP且四边形OAPB是正方形.
①求反比例函数的解析式;
②若动点P在双曲线上运动,作PM⊥x轴交AB于E点;PN⊥y轴交AB于F点.以下有两个结论:AF与BE的积不变,AF与BE的商不变,其中有一个是正确的,请选出正确的结论,并加以证明.
| k |
| x |
①求反比例函数的解析式;
②若动点P在双曲线上运动,作PM⊥x轴交AB于E点;PN⊥y轴交AB于F点.以下有两个结论:AF与BE的积不变,AF与BE的商不变,其中有一个是正确的,请选出正确的结论,并加以证明.

考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据直线的解析式即可求得A、B的坐标,进而求得P的坐标,代入y=
即可求得k的值,从而求得反比例函数的解析式;
(2)分两种情况讨论讨论即可证得.
| k |
| x |
(2)分两种情况讨论讨论即可证得.
解答:解:(1)由直线y=-x+1可知:A(1,0),B(0,1),
∵四边形OAPB是正方形,
∴P(1,1),
代入y=
即可求得k=1,
∴反比例函数的解析式为y=
.
(2)AF与BE的积不变;
如图a,当P运动到P的左侧P1处时,设P1(x,
),则M(1,
),
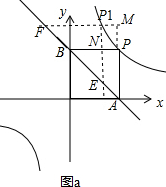
在等腰直角三角形FAM中,AM=
,则AF=
,
在等腰直角三角形NBE中,NB=x,则BE=x
,
所以AF与BE乘积=
•x
=2是定值.
如图b,当P运动到P的左侧P2处时,设P1(x,
),则N(1,
),M(x,1),
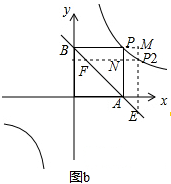
在等腰直角三角形BEM中,BM=x,则BE=x
,
在等腰直角三角形NBE中,NA=
,则FA=
,
所以AF与BE乘积=x
•
=2是定值.
∵四边形OAPB是正方形,
∴P(1,1),
代入y=
| k |
| x |
∴反比例函数的解析式为y=
| 1 |
| x |
(2)AF与BE的积不变;
如图a,当P运动到P的左侧P1处时,设P1(x,
| 1 |
| x |
| 1 |
| x |

在等腰直角三角形FAM中,AM=
| 1 |
| x |
| 1 |
| x |
| 2 |
在等腰直角三角形NBE中,NB=x,则BE=x
| 2 |
所以AF与BE乘积=
| 1 |
| x |
| 2 |
| 2 |
如图b,当P运动到P的左侧P2处时,设P1(x,
| 1 |
| x |
| 1 |
| x |

在等腰直角三角形BEM中,BM=x,则BE=x
| 2 |
在等腰直角三角形NBE中,NA=
| 1 |
| x |
| 1 |
| x |
| 2 |
所以AF与BE乘积=x
| 2 |
| 1 |
| x |
| 2 |
点评:本题考查了反比例函数和一次函数的交点,以及反比例函数图象上点的坐标特征,正方形的性质等,(2)确定出M的坐标是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知方程组
的解是
,则m、n之间的数量关系是( )
|
|
| A、m-16n=5 |
| B、m-16n=11 |
| C、m+16n=-11 |
| D、m+16n=-5 |
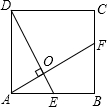 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则| AO |
| DO |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,E是平行四边形ABCD边BC上的一点,且
如图,E是平行四边形ABCD边BC上的一点,且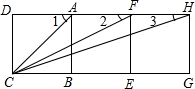 如图所示,三个边长为1个单位长度的正方形ABCD、ABEF、EFHG拼在一起.
如图所示,三个边长为1个单位长度的正方形ABCD、ABEF、EFHG拼在一起.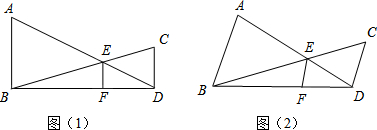
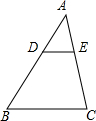 如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为
如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为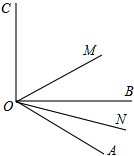 如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.
如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.