题目内容
从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
| 平均数 | 众数 | 方差 | |||
| 甲 | 10 | ||||
| 乙 | 10 |
|
考点:方差,算术平均数,众数
专题:
分析:(1)根据众数、平均数、方差的求法进行计算即可;
(2)可以从不同的方面说,比如:平均数或方差,方差越小,成绩越稳定,答案不唯一.
(2)可以从不同的方面说,比如:平均数或方差,方差越小,成绩越稳定,答案不唯一.
解答:解:(1)甲:12出现的次数最多,所以众数为12,
S甲2=
[(6-10)2+(12-10)2+(8-10)2+(12-10)2+(10-10)2+(12-10)2]=
;
乙:
=
(9+10+11+10+12+8)=10.
故答案为12,
; 10;
(2)解答一:派甲运动员参加比赛,因为甲运动员成绩的众数是12个,大于乙运动员成绩的众数10个,说明甲运动员更容易创造好成绩;
解答二:派乙运动员参加比赛,因为两位运动员成绩的平均数都是10个,而乙成绩的方差小于甲成绩的方差,说明乙运动员的成绩更稳定.
S甲2=
| 1 |
| 6 |
| 16 |
| 3 |
乙:
. |
| x乙 |
| 1 |
| 6 |
故答案为12,
| 16 |
| 3 |
(2)解答一:派甲运动员参加比赛,因为甲运动员成绩的众数是12个,大于乙运动员成绩的众数10个,说明甲运动员更容易创造好成绩;
解答二:派乙运动员参加比赛,因为两位运动员成绩的平均数都是10个,而乙成绩的方差小于甲成绩的方差,说明乙运动员的成绩更稳定.
点评:本题考查了方差、平均数以及众数,是中考的常见题型,要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
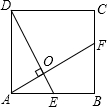 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则| AO |
| DO |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
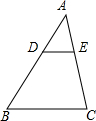 如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为
如图,DE∥BC,AD:DB=2:3,则△AED和△ABC的相似比为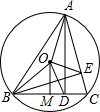 如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.
如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.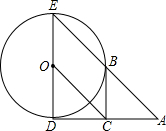 如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.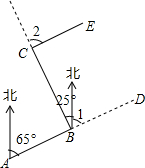 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致? 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为