Question

12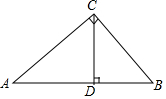．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，且AD：BD=16：9，求sinA的值．

Answer 1

分析 首先根据AD：BD=16：9设AD=16x，则BD=9x，然后利用△ACD∽△CBD求得CD=12x，利用勾股定理求得AC的长，从而利用正弦函数的定义求解即可．

解答 解：∵AD：BD=16：9，
∴设AD=16x，则BD=9x，
∵∠ACB=90°，CD⊥AB，
∴∠CDA=∠CDB=90°，
∵∠A+∠ACD=∠ACD+∠BCD=90°，
∴∠A=∠BCD，
∴△ACD∽△CBD，
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$，
∴CD²=AD•BD=16x•9x，
∴CD=12x，
由勾股定理得：AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{（12x）^{2}+（16x）^{2}}$=20x，
∴sinA=$\frac{CD}{AC}$=$\frac{12x}{20x}$=$\frac{3}{5}$．

点评 本题考查了相似三角形的应用及解直角三角形的知识，解题的关键是能够利用相似三角形的知识求得CD的长，难度中等．