题目内容
3.如图1,E,B,C在同一直线上,四边形ABCD、AEBD都是平行四边形(1)求证:EB=BC;
(2)如图2,连接ED交AB于E,当BE=BD,DC=10,DE=24时,求?ABCD的周长.

分析 (1)根据菱形的判定得出即可;
(2)根据菱形的性质得出AB⊥DE,AF=BF,DF=EF,求出BF和DF,根据勾股定理求出BD,即可求出答案.
解答 (1)证明:∵四边形ABCD、AEBD都是平行四边形,
∴EB=AD,BC=AD,
∴EB=BC;
(2)解:∵四边形ADBE是平行四边形,BE=BD,
∴四边形ADBE是菱形,
∴AB⊥DE,EF=DF,AF=BF,
∵四边形ABCD是平行四边形,DC=10,
∴AB=DC=10,
DF=$\frac{1}{2}$DE=$\frac{1}{2}$×24=12,BF=$\frac{1}{2}$AB=$\frac{1}{2}×$10=5,
在Rt△DFB中,由勾股定理得:BD=$\sqrt{D{F}^{2}+B{F}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∵四边形ADBE是菱形,四边形ABCD是平行四边形,BD=13,
∴AD=BD=DC=BC=13,
∴?ABCD的周长为13×4=52.
点评 本题考查了平行四边形和菱形的性质,菱形的判定和勾股定理等知识点,能求出BD的长是解此题的关键,综合性比较强,难度适中.

练习册系列答案
相关题目
15.若使分式$\frac{{x}^{2}+1}{2x-1}$的值为正数,则x的取值范围是( )
| A. | x$<\frac{1}{2}$ | B. | x$>\frac{1}{2}$ | C. | x$<-\frac{1}{2}$ | D. | x$>-\frac{1}{2}$ |
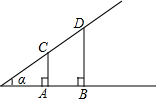 如图,A,B,C,D分别是∠α边上的四个点,且CA,DB均垂直于∠α的一条边,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.
如图,A,B,C,D分别是∠α边上的四个点,且CA,DB均垂直于∠α的一条边,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.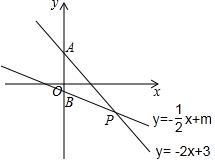 如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于P(n,-2).
如图,函数y=-2x+3与y=-$\frac{1}{2}$x+m的图象交于P(n,-2).
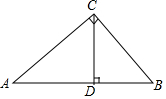 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,且AD:BD=16:9,求sinA的值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,且AD:BD=16:9,求sinA的值.