题目内容
4. 如图,把边长为1的正方形的一个顶点放置在数轴的原点,一边与数轴的正半轴重合,连接对角线OM,再在数轴的正半轴截取ON=OM,则N点所表示的数为$\sqrt{2}$.
如图,把边长为1的正方形的一个顶点放置在数轴的原点,一边与数轴的正半轴重合,连接对角线OM,再在数轴的正半轴截取ON=OM,则N点所表示的数为$\sqrt{2}$.
分析 根据勾股定理,可得OM,根据半径的关系,可得答案.
解答 解:如图 ,
,
在Rt△OMB中,由勾股定理,得
OM=$\sqrt{O{B}^{2}+B{M}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$
ON=OM=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了实数与数轴,利用勾股定理得出OM的长是解题关键.

练习册系列答案
相关题目
15.若使分式$\frac{{x}^{2}+1}{2x-1}$的值为正数,则x的取值范围是( )
| A. | x$<\frac{1}{2}$ | B. | x$>\frac{1}{2}$ | C. | x$<-\frac{1}{2}$ | D. | x$>-\frac{1}{2}$ |
19.下列说法正确的是( )
| A. | 垂线段就是垂直于已知直线的线段 | |
| B. | 垂线段就是垂直于已知直线并且与已知直线相交的线段 | |
| C. | 垂线段是一条竖起来的线段 | |
| D. | 过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段 |
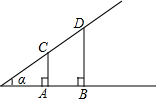 如图,A,B,C,D分别是∠α边上的四个点,且CA,DB均垂直于∠α的一条边,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.
如图,A,B,C,D分别是∠α边上的四个点,且CA,DB均垂直于∠α的一条边,如果CA=AB=2,BD=3,那么tanα=$\frac{1}{2}$.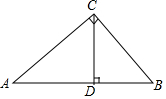 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,且AD:BD=16:9,求sinA的值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,且AD:BD=16:9,求sinA的值.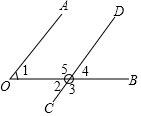 如图,直线CD与∠AOB的边OB相交.
如图,直线CD与∠AOB的边OB相交. 如图,点A,B,C在同一条直线上,点B,D,E在另一条直线上,你能说明∠EBC>∠EFD的理由吗?
如图,点A,B,C在同一条直线上,点B,D,E在另一条直线上,你能说明∠EBC>∠EFD的理由吗?