题目内容
11.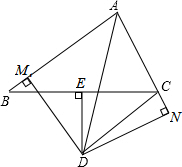 如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.
如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.
分析 因为ED是BC的垂直平分线,那么BD=CD,而AD是∠BAC的平分线,DM⊥AB,DN⊥AC,根据角平分线的性质可得DM=DN,再根据HL可判定Rt△BMD≌Rt△CND,从而有BM=CN.
解答 证明:连接BD,DC,如图: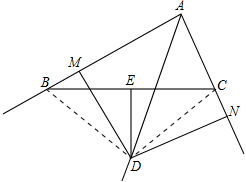
∵DE所在直线是BC的垂直平分线,
∴BD=CD,
∵AD平分∠BAC,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N,
∴DM=DN,
在Rt△BMD与Rt△CDN中,
$\left\{\begin{array}{l}{BD=DC}\\{DM=DN}\end{array}\right.$,
∴Rt△BMD≌Rt△CDN(HL),
∴BM=CN;
点评 本题考查了全等三角形的判定和性质、线段垂直平分线的性质,解题的关键是掌握垂直平分线的定义以及性质,掌握角平分线的性质以及具体的应用.

练习册系列答案
相关题目
3.妈妈买回了一块呈正方体的豆腐,请你帮忙用刀切,规定只能切三刀,你考虑一下,最多能切出豆腐的块数是( )
| A. | 4块 | B. | 6块 | C. | 8块 | D. | 10块 |
1.在平行四边形ABCD,AB=3,BC=5,则平行四边形ABCD的周长为( )
| A. | 8 | B. | 12 | C. | 14 | D. | 16 |
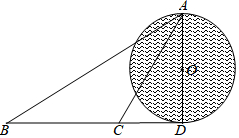 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°.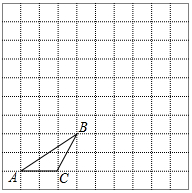 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).