题目内容
10.阅读下文,寻找规律:已知x≠1时,(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4…
(1)填空:(1-x)(1+x+x2+x3+x4)=1-x5.
(2)观察上式,并猜想:
①(1-x)(1+x+x2+…+xn)=1-xn+1.
②(x-1)(x10+x9+…+x+1)=x11-1.
(3)根据你的猜想,计算:
①(1-2)(1+2+22+23+24+25)=1-26.
②1+3+32+33+34…32016=$\frac{{{3^{2017}}-1}}{2}$.
分析 (1)根据规律即可得到结论;
(2)根据规律即可得到结论;
(3)①先设S=1+2+22+23+24+25,再将等式的两边同时乘以2,将两式相减即可;②首先根据已知设S=1+3+32+33+…+32015+32016,①再将其两边同乘3得到关系式②,②-①即可求得答案.
解答 解:(1)(1-x)(1+x+x2+x3+x4)=1-x5.
故答案为:1+x+x2+x3+x4;
(2)①(1-x)(1+x+x2+…+xn)=1-xn+1;
②(x-1)(x10+x9+…+x+1)=x11-1;
故答案为:1-xn+1;x11-1;
(3)①解:设S=1+2+22+23+24+25①,
将等式两边同时乘以2得:2S=2+22+23+24+25+26②,
②-①得,2S-S=26-1,即S=26-1,
即1+2+22+23+24+25=26-1.
设S=1+3+32+33+…+32015+32016,①
①×3得3S=3+32+33+3…32016+32017,②
②-①得:2s=32017-1,S=$\frac{{3}^{2017}-1}{2}$.
故答案为:26-1,$\frac{{{3^{2017}}-1}}{2}$.
点评 本题考查了有理数的乘方,读懂题目信息,理解求和的运算方法是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 100 | 60 |
| 乙型挖掘机 | 120 | 80 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
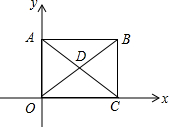 已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A点的坐标为(0,2),则点D的坐标为($\sqrt{3}$,1).
已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A点的坐标为(0,2),则点D的坐标为($\sqrt{3}$,1).