题目内容
18.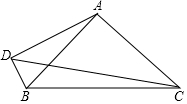 如图,己知∠CAB=90°,AB=$\frac{\sqrt{2}}{2}$BC,AD⊥BD,S△ABD=$\frac{3}{40}$BC2,sin∠CDB=$\frac{\sqrt{2}}{2}$.
如图,己知∠CAB=90°,AB=$\frac{\sqrt{2}}{2}$BC,AD⊥BD,S△ABD=$\frac{3}{40}$BC2,sin∠CDB=$\frac{\sqrt{2}}{2}$.
分析 作AE⊥BC于E,由题意可知△ABC是等腰直角三角形,且A,D,B,E四点共圆,从而可知sin∠CDB=sin∠BAE=$\frac{\sqrt{2}}{2}$.
解答  解:作AE⊥BC于E,
解:作AE⊥BC于E,
∵∠CAB=90°,AB=$\frac{\sqrt{2}}{2}$BC,
∴cos∠ABC=$\frac{AB}{BC}$=$\frac{\sqrt{2}}{2}$,
∴∠ABC=45°,
∴△ABC是等腰直角三角形,
∵AE⊥BC,
∴∠BAE=45°,
∵AD⊥BD,
∴∠ADB=∠AEB=90°,
∴A,D,B,E四点共圆,
∴∠CDB=∠BAE=45°,
∴sin∠CDB=sin∠BAE=$\frac{\sqrt{2}}{2}$
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题考查解直角三角形,涉及圆周角定理,等腰直角三角形的判定,锐角三角函数,本题属于中等题型.

练习册系列答案
相关题目
9. 如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1的度数是( )
如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1的度数是( )
 如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1的度数是( )
如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1的度数是( )| A. | 30° | B. | 25° | C. | 20° | D. | 15° |
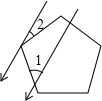 如图,一束平行太阳光照射到正五边形上,若∠1=44°,则∠2=28°.
如图,一束平行太阳光照射到正五边形上,若∠1=44°,则∠2=28°. 如图,在平面直角坐标系中的三点A(1,0),B(-1,0),P(0,-1),将线段AB沿y轴向上平移m(m>0)个单位长度,得到线段CD,二次函数y=a(x-h)2+k的图象经过点P、C、D.
如图,在平面直角坐标系中的三点A(1,0),B(-1,0),P(0,-1),将线段AB沿y轴向上平移m(m>0)个单位长度,得到线段CD,二次函数y=a(x-h)2+k的图象经过点P、C、D. 如图,在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线CF∥AB,D为AB边上一点,DE⊥BC于E交CF于点F.连结BF,CD.
如图,在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线CF∥AB,D为AB边上一点,DE⊥BC于E交CF于点F.连结BF,CD. 如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为∠DAB=90°(填一个即可).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为∠DAB=90°(填一个即可).