题目内容
9．
如图，将一副直角三角板按图中所示位置摆放，保持两条斜边互相平行，则∠1的度数是（ ）| A． | 30° | B． | 25° | C． | 20° | D． | 15° |
分析 根据平行线的性质可得∠C=∠2=60°，再根据三角形内角与外角的性质可得∠1的度数．
解答 
解：∵AB∥CD，
∴∠C=∠2=60°，
∵∠A=45°，
∴∠1=60°-45°=15°，
故选：D．
点评 此题主要考查了平行线的性质，关键是掌握两直线平行，同位角相等．
练习册系列答案
相关题目
19．下列说法正确的是（ ）
| A． | 0.720精确到0.01 | B． | 5.078精确到千分位 | ||
| C． | 3.6万精确到十分位 | D． | 3000精确到千位 |
20．某图纸上注明：一种零件的直径是$30_{-0.02}^{+0.03}$mm，下列尺寸合格的是（ ）
| A． | 30.01mm | B． | 30.05mm | C． | 29.08mm | D． | 29.97mm |
17．如果y=（1-m）x${\;}^{{m}^{2}-2}$是正比例函数，且y随x的增大而减小，则m的值为（ ）
| A． | m=-$\sqrt{3}$ | B． | m=$\sqrt{3}$ | C． | m=3 | D． | m=-3 |
14．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | 2a2+a2=3a4 | C． | a6÷a3=a2 | D． | （ab2）3=a3b6 |
17．某水果基地计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水果）．下表为装运甲、乙、丙三种水果的重量及利润．
（1）用8辆汽车装运乙、丙两种水果共22吨到A地销售，问装运乙、丙两种水果的汽车各多少辆？
（2）水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售（每种水果不少于一车），假设装运甲水果的汽车为m辆，则装运乙、丙两种水果的汽车各多少辆？（结果用m表示）
（3）在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？
| 甲 | 乙 | 丙 | |
| 每辆汽车能装的数量（吨）） | 4 | 2 | 3 |
| 每吨水果可获利润（千元） | 5 | 7 | 4 |
（2）水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售（每种水果不少于一车），假设装运甲水果的汽车为m辆，则装运乙、丙两种水果的汽车各多少辆？（结果用m表示）
（3）在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？
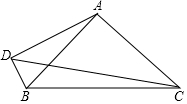如图，己知∠CAB=90°，AB=$\frac{\sqrt{2}}{2}$BC，AD⊥BD，S△ABD=$\frac{3}{40}$BC2，sin∠CDB=$\frac{\sqrt{2}}{2}$．