题目内容
8.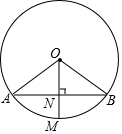 如图,在⊙O中,半径OM垂直弦AB于点N.
如图,在⊙O中,半径OM垂直弦AB于点N.(1)若AB=2$\sqrt{3}$,ON=1,求MN的长;
(2)若AB=2$\sqrt{3}$,MN=1,求ON的长.
分析 (1)根据垂经定理,可得AN的长,根据勾股定理,可得OA,根据线段的和差,可得答案;
(2)根据垂经定理,可得AN的长,根据勾股定理,可得ON.
解答 解:(1)由垂经定理,得
AN=$\frac{1}{2}$AB=$\sqrt{3}$,
由勾股定理,得
AO=$\sqrt{A{N}^{2}+O{N}^{2}}$=2,
MN=MO-ON=2-1=1;
(2)AO=x,ON=x-1.
由勾股定理,得
x=$\sqrt{(\sqrt{3})^{2}+(x-1)^{2}}$,
x=2,
ON=OM-MN=2-1=1.
点评 本题考查了垂经定理,利用垂经定理是解题关键.

练习册系列答案
相关题目
18.已知a-3b=4,ab=2,则式子3ab-2a+6b的值等于( )
| A. | 0 | B. | 2 | C. | -4 | D. | -2 |
 如图,已知△ABC中,AB=AC=5,BC=6.
如图,已知△ABC中,AB=AC=5,BC=6.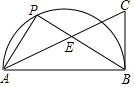 如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为$\frac{6}{5}$.
如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为$\frac{6}{5}$.