题目内容
12.抛物线y=x2+mx+4与x轴仅有一个交点,则该交点的坐标是(-2,0)或(2,0).分析 因为抛物线y=x2+mx+4与x轴仅有一个交点,可知△=0,列出方程求出m,再求出抛物线与x轴的交点坐标即可.
解答 解:∵抛物线y=x2+mx+4与x轴仅有一个交点,
∴△=0,
∴m2-16=0,
∴m=±4,
∴抛物线的解析式为y=x2+4x+4或y=x2-4x+4,
∴抛物线由x轴的交点坐标为(-2,0)或(2,0),
故答案为(-2,0)或(2,0).
点评 本题考查抛物线与x轴的交点坐标、记住△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点,属于中考常考题型.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
2. 如图,设线段AC=1.过点C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:连结AD,以点D为圆心,DC的长为半径画弧,交AD于点E;再以点A为圆心,AE的长为半径画弧,交AC于点B,则AB的长为( )
如图,设线段AC=1.过点C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:连结AD,以点D为圆心,DC的长为半径画弧,交AD于点E;再以点A为圆心,AE的长为半径画弧,交AC于点B,则AB的长为( )
 如图,设线段AC=1.过点C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:连结AD,以点D为圆心,DC的长为半径画弧,交AD于点E;再以点A为圆心,AE的长为半径画弧,交AC于点B,则AB的长为( )
如图,设线段AC=1.过点C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:连结AD,以点D为圆心,DC的长为半径画弧,交AD于点E;再以点A为圆心,AE的长为半径画弧,交AC于点B,则AB的长为( )| A. | $\frac{2\sqrt{5}-1}{5}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{4}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
20.有一人患了红眼病,经过两轮传染后共有144人患了红眼病,那每轮传染中平均一个人传染的人数为( )人.
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
7.下列方程是一元二次方程的是( )
| A. | x2+x=3 | B. | $\frac{1}{{x}^{2}}$+x=3 | C. | $\sqrt{{x}^{2}+1}$-1=x | D. | x2+y=6 |
17.将抛物线y=x2平移得到抛物线y=(x-3)2,则这个平移过程正确的是( )
| A. | 向左平移3个单位 | B. | 向右平移3个单位 | C. | 向上平移3个单位 | D. | 向下平移3个单位 |
4.下列方程中属于一元一次方程的是( )
| A. | y2=4 | B. | 2+$\frac{y}{2}$=6 | C. | x2+x+1=0 | D. | x-2y=1 |
2. 如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )
如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )
 如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )
如图,在⊙O中,∠ABC=50°,则∠AEC的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 50° |
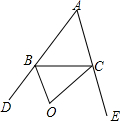 如图,O是外角∠DBC的平分线BO与外角∠ECB的平分线CO的交点,则∠BOC与∠A的关系是∠BOC=90°+$\frac{1}{2}$∠A.
如图,O是外角∠DBC的平分线BO与外角∠ECB的平分线CO的交点,则∠BOC与∠A的关系是∠BOC=90°+$\frac{1}{2}$∠A.