题目内容
1.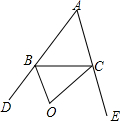 如图,O是外角∠DBC的平分线BO与外角∠ECB的平分线CO的交点,则∠BOC与∠A的关系是∠BOC=90°+$\frac{1}{2}$∠A.
如图,O是外角∠DBC的平分线BO与外角∠ECB的平分线CO的交点,则∠BOC与∠A的关系是∠BOC=90°+$\frac{1}{2}$∠A.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠OBC和∠OCB,再根据三角形的内角和等于180°列式表示出∠BOC,然后整理即可得解.
解答 解:由三角形的外角性质得,∠CBD=∠A+∠ACB,
∠BCE=∠A+∠ABC,
∵OB、OC分别是∠DBC和∠ECB的平分线,
∴∠OBC=$\frac{1}{2}$∠CBD=$\frac{1}{2}$(∠A+∠ACB),
∠OCB=$\frac{1}{2}$∠BCE=$\frac{1}{2}$(∠A+∠ABC),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC),
在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC=$\frac{1}{2}$(180°+∠A)=90°+$\frac{1}{2}$∠A.
即∠BOC=90°+$\frac{1}{2}$∠A.
故答案为:∠BOC=90°+$\frac{1}{2}$∠A.
点评 本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,三角形的内角和定理,熟记性质与定理并理清图中各角度之间的关系是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
11.在实数-$\frac{2}{5}$、0、-$\sqrt{3}$、2015、π、-$\root{3}{-27}$、0.1$\stackrel{•}{0}$$\stackrel{•}{1}$中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.二次函数y=2x2-3x+4的最值情况为( )
| A. | 当x=-$\frac{3}{4}$时取得最大值为$\frac{23}{8}$ | B. | 当x=-$\frac{3}{4}$时取得最小值为$\frac{23}{8}$ | ||
| C. | 当x=$\frac{3}{4}$时取得最大值为$\frac{23}{8}$ | D. | 当x=$\frac{3}{4}$时取得最小值为$\frac{23}{8}$ |
6.经过某丁字路口的汽车,可能向左转,也可能向右转,如果这两种可能性大小相同,当有三辆汽车经过这个丁字路口时,三辆汽车全部左拐的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{27}$ |
11.下列实数中属于无理数的是( )
| A. | 3.1415 | B. | -$\frac{π}{3}$ | C. | $\frac{22}{7}$ | D. | $\frac{3}{5}$ |
 如图,已知在直角坐标系中,点P是直线y=-x+4上的一个动点,⊙O的半径为1,过点P作⊙O的切线,切点为A,则PA长度的最小值为$\sqrt{7}$.
如图,已知在直角坐标系中,点P是直线y=-x+4上的一个动点,⊙O的半径为1,过点P作⊙O的切线,切点为A,则PA长度的最小值为$\sqrt{7}$.