题目内容
2. 如图,设线段AC=1.过点C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:连结AD,以点D为圆心,DC的长为半径画弧,交AD于点E;再以点A为圆心,AE的长为半径画弧,交AC于点B,则AB的长为( )
如图,设线段AC=1.过点C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:连结AD,以点D为圆心,DC的长为半径画弧,交AD于点E;再以点A为圆心,AE的长为半径画弧,交AC于点B,则AB的长为( )| A. | $\frac{2\sqrt{5}-1}{5}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{4}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
分析 根据题意,作出图形.根据勾股定理求得AD的长度,则AB=AE=AD-CD.
解答 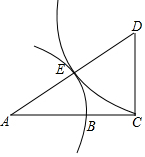 解:如图,AC=1,CD=$\frac{1}{2}$AC=$\frac{1}{2}$,CD⊥AC,
解:如图,AC=1,CD=$\frac{1}{2}$AC=$\frac{1}{2}$,CD⊥AC,
∴由勾股定理,得
AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$.
又∵DE=DC=$\frac{1}{2}$,
∴AB=AE=AD-CD=$\frac{\sqrt{5}}{2}$-$\frac{1}{2}$=$\frac{\sqrt{5}-1}{2}$.
故选:B.
点评 本题考查了勾股定理.根据勾股定理求得斜边AD的长度是解题的关键.

练习册系列答案
相关题目
7.我们约定:如果身高在166(单位:cm)的±2%范围之内都称为“普通身高”.下面10名男生中的身高(单位:cm)
具有“普通身高”的有几人( )
| 男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高x(cm) | 163 | 171 | 173 | 156 | 161 | 174 | 164 | 166 | 169 | 164 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 最大整数解是 ( )
最大整数解是 ( ) = _____ ,(x+2y﹣3)(x﹣2y+3) = ___________
= _____ ,(x+2y﹣3)(x﹣2y+3) = ___________ 勾股定理是世界上最伟大的定理之一,是用代数思想解决几何问题的重要工具,也是数形结合的纽带,周老师在上八年级《从勾股定理到图形面积关系的拓展》一节拓展课时,教学环节清晰,内容安排有序,问题设计合理(如下),作为课堂主人的你,请积极思考解决下列问题:
勾股定理是世界上最伟大的定理之一,是用代数思想解决几何问题的重要工具,也是数形结合的纽带,周老师在上八年级《从勾股定理到图形面积关系的拓展》一节拓展课时,教学环节清晰,内容安排有序,问题设计合理(如下),作为课堂主人的你,请积极思考解决下列问题: