题目内容
13.实数$\frac{22}{7}$,cos60°,$\sqrt{2}$-1,$\frac{π}{3}$,($\sqrt{3}$)0,$\root{3}{-8}$,$\sqrt{12}$,|-3|,0.1010010001…中,无理数的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:无理数有:$\sqrt{2}$-1,$\frac{π}{3}$,$\sqrt{12}$,0.1010010001…共4个.
故选C.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
相关题目
3.下列各式计算正确的是( )
| A. | a2+a2=2a4 | B. | a5-a2=a3 | C. | 3a+b=3ab | D. | -x2y+yx2=0 |
18.下列运算正确的是( )
| A. | $\frac{-x-y}{-x+y}$=$\frac{x-y}{x+y}$ | B. | $\frac{y-x}{(x-y)^{2}}$=$\frac{1}{x-y}$ | ||
| C. | $\frac{{x}^{2}-{y}^{2}}{(y-x)^{2}}$=$\frac{x+y}{x-y}$ | D. | $\frac{y-x}{{x}^{2}-{y}^{2}}$=$\frac{1}{x+y}$ |
2.下面各数中,既是分数,又是正数的是( )
| A. | 5 | B. | -2.25 | C. | 0 | D. | 8.3 |
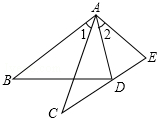 如图,在△ABD和△ACE中,有下列四个等式:①AB=AC、②AD=AE、③∠1=∠2、④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个真命题(要求写出已知,求证及证明过程)题设:①②③,结论:④(写序号)
如图,在△ABD和△ACE中,有下列四个等式:①AB=AC、②AD=AE、③∠1=∠2、④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个真命题(要求写出已知,求证及证明过程)题设:①②③,结论:④(写序号)