题目内容
12.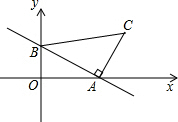 如图,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°
如图,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°(1)求点C的坐标;
(2)求过B、C两点的直线的解析式.
分析 (1)先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标;
(2)用待定系数法即可求出直线BC的解析式.
解答 解:(1)∵一次函数y=-$\frac{2}{3}$x+2中,
令x=0得:y=2;令y=0,解得x=3,
∴B的坐标是(0,2),A的坐标是(3,0).
如图,作CD⊥x轴于点D.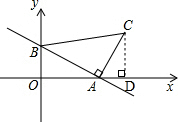
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO与△CAD中,
∵$\left\{\begin{array}{l}{∠BAO=∠ACD}\\{∠BOA=∠ADC=90°}\\{AB=AC}\end{array}\right.$,
∴△ABO≌△CAD(AAS),
∴OB=AD=2,OA=CD=3,OD=OA+AD=5.
则C的坐标是(5,3).
(2)设直线BC的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{5k+b=3}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=2}\end{array}\right.$,
∴直线BC的解析式是y=$\frac{1}{5}$x+2.
点评 本题考查的是待定系数法求一次函数的解析式、全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
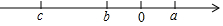 已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.