Question

16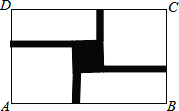．如图，某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭，观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路，已知道路的宽为正方形边长的$\frac{1}{4}$，若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$，求道路的宽．

Answer 1

分析 首先假设道路的宽为x米，根据道路的宽为正方形边长的$\frac{1}{4}$，得出正方形的边长以及道路与正方形的面积进而得出答案．

解答 解：设道路的宽为x米，
则可列方程：
x（24-4x）+x（40-4x）+16x²=$\frac{1}{6}$×40×24，
即：x²+4x-5=0，
解得：x₁=l，x₂=-5（舍去）．
答：道路的宽为1米．

点评 此题主要考查了一元二次方程的应用，根据已知表示出阴影部分的面积是解题关键．