题目内容
4．解方程：x3-2=6．分析 由x3-2=6，首先求得x3=8，又由23=8，即可求得答案．
解答 解：∵x3-2=6，
∴x3=8，
∴x=2．
点评 此题考查了立方根的定义．注意首先求得x3是解此题的关键．
练习册系列答案
相关题目
14．函数y=$\frac{x-1}{\sqrt{x-2}}$中自变量x的取值范围是（ ）
| A． | x＞2 | B． | x≠2 | C． | x≥2且x≠1 | D． | x为任意实数 |
19．
如图，在菱形ABCD中，EF⊥AC于点G，分别交AD及CB的延长线于点E、F交AB于点H，AH：FB=1：2，则AG：GC的值为（ ）
如图，在菱形ABCD中，EF⊥AC于点G，分别交AD及CB的延长线于点E、F交AB于点H，AH：FB=1：2，则AG：GC的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{4}$ |
9．抛物线y=-2x2-3与双曲线y=-$\frac{1}{x}$的交点所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
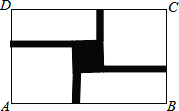如图，某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭，观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路，已知道路的宽为正方形边长的$\frac{1}{4}$，若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$，求道路的宽．
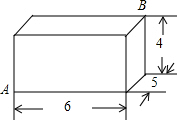如图，有一个长方体盒子，长、宽、高分别为6cm、5cm、4cm，有一只小虫要从点A处沿长方体表面爬到点B处，最短的路径长为$\sqrt{117}$cm．