��Ŀ����
7�� ����ͼ�ķ����У�ÿ��С�����εı߳���Ϊ1����ABC�Ķ�����ڸ���ϣ��ڽ���ƽ��ֱ������ϵ��B������Ϊ��-1��2����
����ͼ�ķ����У�ÿ��С�����εı߳���Ϊ1����ABC�Ķ�����ڸ���ϣ��ڽ���ƽ��ֱ������ϵ��B������Ϊ��-1��2������1���ѡ�ABC����ƽ��8����λ��õ���Ӧ�ġ�A1B1C1��������A1B1C1��
��2���������A1B1C1����y��ԳƵġ�A2B2C2��
��3������P��a��b���ǡ�ABC��������һ�㣬P2�ǡ�A2B2C2������P��Ӧ�ĵ㣬д��P2������Ϊ��-a��b-8����
��4������y������һ��Q��ʹ�õ�Q��B2��C2����ľ���֮����С����ʱ��QB2+QC2����СֵΪ3$\sqrt{2}$��
���� ��1���ֱ�A��B��C����ƽ��8����λ��Ȼ��˳�����ӣ�
��2���ֱ�������A1��B1��C1����y��ԳƵĵ㣬Ȼ��˳�����ӣ�
��3����������ͼ��д��P2�����ꣻ
��4��������B2����y��ĶԳƵ�B1������B1C2����y��Ľ��㼴Ϊ��Q��Ȼ�������Сֵ��
���  �⣺��1������ͼ����ͼ��ʾ��
�⣺��1������ͼ����ͼ��ʾ��
��2������ͼ����ͼ��ʾ��
��3��P2��������-a��b-8����
��4����Q��ͼ��ʾ��
QB2+QC2=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$��
�ʴ�Ϊ����-a��b-8����3$\sqrt{2}$��
���� ���⿼���˸�����ԳƱ任��ƽ�Ʊ任��ͼ�������Ĺؼ��Ǹ�������ṹ������Ӧ���λ�ã�Ȼ��˳�����ӣ�

��ϰ��ϵ�д�
�����Ŀ
18����֪a+$\frac{1}{a}$=$\sqrt{5}$����a-$\frac{1}{a}$=��������
| A�� | 1 | B�� | -1 | C�� | ��1 | D�� | -$\sqrt{5}$ |
19�� ��ͼ��������ABCD�У�EF��AC�ڵ�G���ֱ�AD��CB���ӳ����ڵ�E��F��AB�ڵ�H��AH��FB=1��2����AG��GC��ֵΪ��������
��ͼ��������ABCD�У�EF��AC�ڵ�G���ֱ�AD��CB���ӳ����ڵ�E��F��AB�ڵ�H��AH��FB=1��2����AG��GC��ֵΪ��������
 ��ͼ��������ABCD�У�EF��AC�ڵ�G���ֱ�AD��CB���ӳ����ڵ�E��F��AB�ڵ�H��AH��FB=1��2����AG��GC��ֵΪ��������
��ͼ��������ABCD�У�EF��AC�ڵ�G���ֱ�AD��CB���ӳ����ڵ�E��F��AB�ڵ�H��AH��FB=1��2����AG��GC��ֵΪ��������| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{2}{5}$ | D�� | $\frac{1}{4}$ |
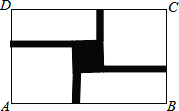 ��ͼ��ij���ξ���Ҫ�ڳ������ֱ�Ϊ40m��24m�ľ���ˮ�ص������뽨��һ������εĸ�����ƽ�е������ι���ͤ������ͤ���ı�������������εı���ƽ���ҿ�����ȵĵ�·����֪��·�Ŀ�Ϊ�����α߳���$\frac{1}{4}$������·�����ͤ�����֮���Ǿ���ˮ�������$\frac{1}{6}$�����·�Ŀ���
��ͼ��ij���ξ���Ҫ�ڳ������ֱ�Ϊ40m��24m�ľ���ˮ�ص������뽨��һ������εĸ�����ƽ�е������ι���ͤ������ͤ���ı�������������εı���ƽ���ҿ�����ȵĵ�·����֪��·�Ŀ�Ϊ�����α߳���$\frac{1}{4}$������·�����ͤ�����֮���Ǿ���ˮ�������$\frac{1}{6}$�����·�Ŀ���