题目内容
11．解方程：2x2-4x-9=0（用配方法解）．分析 方程二次项系数化为1，常数项移到右边，两边加上一次项系数一半的平方，变形后开方即可求出解．
解答 解：由原方程，得
2（x2-2x+1）=11，
x2-2x+1=$\frac{11}{2}$，
（x-1）2=$\frac{11}{2}$，
解得x1=1+$\frac{\sqrt{22}}{2}$，x1=1-$\frac{\sqrt{22}}{2}$．
点评 此题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
19．
如图，在菱形ABCD中，EF⊥AC于点G，分别交AD及CB的延长线于点E、F交AB于点H，AH：FB=1：2，则AG：GC的值为（ ）
如图，在菱形ABCD中，EF⊥AC于点G，分别交AD及CB的延长线于点E、F交AB于点H，AH：FB=1：2，则AG：GC的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{4}$ |
6．
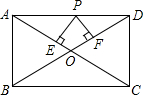如图，在矩形ABCD中，AB=3，AD=4，P是AD上不与A、D重合的一动点，PE⊥AC，PF⊥BD，E、F为垂足，则PE+PF的值为（ ）
如图，在矩形ABCD中，AB=3，AD=4，P是AD上不与A、D重合的一动点，PE⊥AC，PF⊥BD，E、F为垂足，则PE+PF的值为（ ）| A． | 2 | B． | 2.4 | C． | 2.5 | D． | 2.6 |
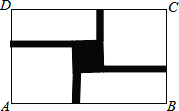如图，某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭，观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路，已知道路的宽为正方形边长的$\frac{1}{4}$，若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$，求道路的宽．
3．△ABC中，BC=AC，D是AB上一点，连结CD，且AD=BD=CD，则∠A的度数为（ ）
| A． | 45° | B． | 36° | C． | 90° | D． | 135° |