题目内容
6.使得关于x的不等式组$\left\{\begin{array}{l}x>m-2\\-2x+1≥4m-1\end{array}\right.$有解,且使分式方程$\frac{1}{x-2}-\frac{m-x}{2-x}=2$有非负整数解的所有的m的和是( )| A. | -1 | B. | 2 | C. | -7 | D. | 0 |
分析 根据不等式组的解集的情况得出关于m的不等式,求得m的解集,再解分式方程得出x,根据x是非负整数得出m所有的m的和.
解答 解:∵关于x的不等式组$\left\{\begin{array}{l}x>m-2\\-2x+1≥4m-1\end{array}\right.$有解,
∴1-2m>m-2,
解得m<1,
由$\frac{1}{x-2}-\frac{m-x}{2-x}=2$得x=$\frac{m+5}{3}$,
∵分式方程$\frac{1}{x-2}-\frac{m-x}{2-x}=2$有非负整数解,
∴x=$\frac{m+5}{3}$是非负整数,
∵m<1,
∴m=-5,-2,
∴-5-2=-7,
故选C.
点评 本题考查了分式方程的解以及不等式的解集,求得m的取值范围以及解分式方程是解题的关键.

练习册系列答案
相关题目
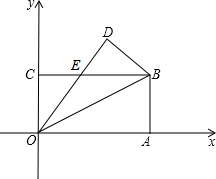 如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.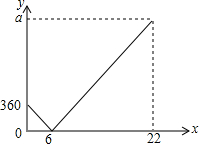 小明家、小芳家与人民公园依次在一条直线上,小明、小芳两人同时各自从家沿直线匀速步行到人民公园,已知小明到达公园花了22分钟,小芳的步行速度是40米/分钟,设两人出发x(分钟)后,小明离小芳家的距离为y(米),y与x的函数关系如图所示.
小明家、小芳家与人民公园依次在一条直线上,小明、小芳两人同时各自从家沿直线匀速步行到人民公园,已知小明到达公园花了22分钟,小芳的步行速度是40米/分钟,设两人出发x(分钟)后,小明离小芳家的距离为y(米),y与x的函数关系如图所示.