题目内容
11.(1)解不等式组$\left\{\begin{array}{l}{x+4>0}\\{2x+5<1}\end{array}\right.$,并把解集在数轴上表示出来.(2)已知:关于x的方程$\frac{a}{x+1}$=1的解是(1)中不等式组的整数解,求a的值.
分析 (1)先解不等式,再求解集的公共部分即可;
(2)把x的值代入即可得出a的值.
解答 解:(1)解x+4>0得x>-4,
解2x+5<1得x<-2,
不等式组的解集为-4<x<-2,
把解集画在数轴上: ;
;
(2)∵不等式组$\left\{\begin{array}{l}{x+4>0}\\{2x+5<1}\end{array}\right.$,的解集为-4<x<-2,
∴整数解为x=-3,
把x=-3代入方程$\frac{a}{x+1}$=1,得$\frac{a}{-3+1}$=1,
∴a=-2,
∴a的值为-2.
点评 本题考查了解不等式组以及解方程,求得不等式组的解集是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.2的倒数的相反数是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |

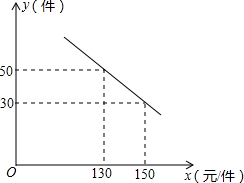 某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系: