题目内容
1. 给下面命题的说理过程填写依据.
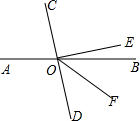
给下面命题的说理过程填写依据.已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=$\frac{1}{2}$∠BOC说明理由.
理由:因为∠AOC=∠BOD(对顶角相等),
∠BOF=$\frac{1}{2}$∠BOD(角平分线的定义),
所以∠BOF=$\frac{1}{2}$∠AOC(等量代换)
因为∠AOC=180°-∠BOC(平角得的定义),
所以∠BOF=90°-$\frac{1}{2}$∠BOC.
因为EO⊥CD(已知),
所以∠COE=90°(垂直的定义)
因为∠BOE+∠COE=∠BOC(两角和的定义),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°(等量代换)
因为∠EOF=∠BOE+∠BOF(两角和的定义)
所以∠EOF=(∠BOC-90°)+(90°-$\frac{1}{2}$∠BOC)(等量代换)
所以∠EOF=$\frac{1}{2}$∠BOC.
分析 根据对顶角的性质得到∠AOC=∠BOD,由角平分线的定义得到∠BOF=$\frac{1}{2}$∠BOD,等量代换得到∠BOF=$\frac{1}{2}$∠AOC,由垂直的定义得到∠COE=90°,等量代换得到∠BOE=∠BOC-90°,于是得到结论.
解答 解:因为∠AOC=∠BOD(对顶角相等),
∠BOF=$\frac{1}{2}$∠BOD(平分线的定义),
所以∠BOF=$\frac{1}{2}$∠AOC(等量代换)
因为∠AOC=180°-∠BOC(平角的定义),
所以∠BOF=90°-$\frac{1}{2}$∠BOC.
因为EO⊥CD(已知),
所以∠COE=90°(垂直的定义)
因为∠BOE+∠COE=∠BOC(两角和的定义),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°(等量代换)
因为∠EOF=∠BOE+∠BOF(两角和的定义)
所以∠EOF=(∠BOC-90°)+(90°-$\frac{1}{2}$∠BOC)(等量代换)
所以∠EOF=$\frac{1}{2}$∠BOC.
故答案为:对顶角相等,角平分线的定义,等量代换,平角的定义,已知,垂直的定义,两角和的定义,等量代换,两角和的定义,等量代换.
点评 本题考查了对顶角、邻补角、垂线以及角平分线的定义;弄清各个角之间的关系是解题的关键.

练习册系列答案
相关题目
13. 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )| A. | abc>0 | B. | a+b+c<0 | C. | b<a+c | D. | 4a+2b+c>0 |
11. 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
通过描点连线,观察并求出I与R之间的函数关系式.
 张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:
张华同学在一次做电学实验时,记录下电流I(安)与电阻R(欧)有如表对应关系:| R | … | 2 | 4 | 8 | 10 | 16 | … |
| I | … | 16 | 8 | 4 | 3.2 | 2 | … |
 如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°.
如图,直线AB与x轴的负半轴、y轴的正半轴分别交于点A、点B,M为线段AB的中点,以OM为直径的⊙P分别交x轴、y轴于点C、点D,交直线AB于点E,OB=8,∠OAB=30°. 如图,写出平面直角坐标系中点A,B,C,D,E,F的坐标.
如图,写出平面直角坐标系中点A,B,C,D,E,F的坐标.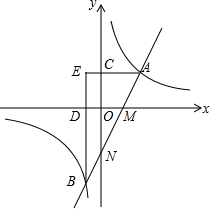 如图,直线y=2x-2分别与x轴、y轴相交于M,N两点,并且与双曲线y=$\frac{k}{x}$(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
如图,直线y=2x-2分别与x轴、y轴相交于M,N两点,并且与双曲线y=$\frac{k}{x}$(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).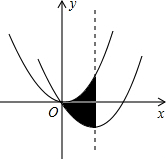 如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.