题目内容
10.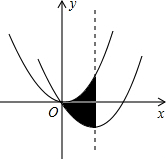 如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
分析 过B作BC⊥y轴于C,根据抛物线的对称性可知阴影部分的面积等于矩形OABC的面积,然后求解即可.
解答 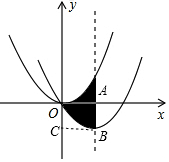 解:过B作BC⊥y轴于C,
解:过B作BC⊥y轴于C,
根据平移得:x轴上面的阴影部分的面积等于四边形OABC中空白部分的面积,则对称轴与两段抛物线所围成的阴影部分的面积等于四边形OABC的面积,
y=$\frac{1}{2}$x2-2x=$\frac{1}{2}$(x2-4x+4-4)=$\frac{1}{2}$(x-2)2-2,
∵点B是抛物线y=$\frac{1}{2}$x2-2x的顶点,
∴B(2,-2),
∴AB=2,BC=2,
∵四边形OABC为矩形,
∴S四边形OABC=2×2=4,
即对称轴与两段抛物线所围成的阴影部分的面积等于4,
故答案为:4.
点评 本题考查了阴影部分面积的求法,观察图形,将阴影部分的图形转化为与它相等的四边形或三角形是解题的关键.

练习册系列答案
相关题目
18.甲、乙两班学生到集市上购买苹果,苹果的价格如表:
甲班分两次购买60千克(第二次多于第一次),而乙班一次购买苹果60千克.
(1)若甲班第一次购买28千克,第二次购买32千克,则乙班比甲班少付多少元?
(2)若甲班两次共付费163元,则甲班第一次、第二次分别购买苹果多少千克?
| 所购苹果数量 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
(1)若甲班第一次购买28千克,第二次购买32千克,则乙班比甲班少付多少元?
(2)若甲班两次共付费163元,则甲班第一次、第二次分别购买苹果多少千克?
19.已知a是一个两位数,b是一个三位数,若把a写在b的左边得到一个五位数记为P,把a写在b的右边得到一个五位数记为H,则P-H等于( )
| A. | 9a-9b | B. | 99a-b | C. | 999a-9b | D. | 999a-99b |
 给下面命题的说理过程填写依据.
给下面命题的说理过程填写依据. 将两个全等的直角三角形,拼成一个四边形.那么这些图形中有4个轴对称图形.
将两个全等的直角三角形,拼成一个四边形.那么这些图形中有4个轴对称图形.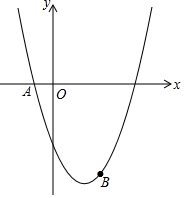 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).