题目内容
20.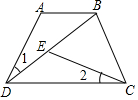 如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC,
如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC,(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.
分析 (1)根据两角夹边对应相等的两个三角形全等即可证明.
(2)利用全等三角形的性质即可解决问题.
解答 (1)证明:∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{DB=DC}\\{∠ABD=∠EDC}\end{array}\right.$,
∴△ABD≌△EDC(ASA).
(2)∵△ABD≌△EDC,
∴∠DEC=∠A=135°,
∵∠BDC=30°,DB=DC,
∴∠DBC=∠DCB=75°,∠2=180°-135°-30°=15°,
∴∠BCE=75°-15°=60°.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质等这是,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
10.如果方程2x-6=0,那么3x+8的值( )
| A. | 11 | B. | 14 | C. | 17 | D. | 20 |
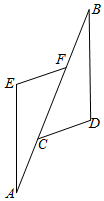 如图,A、C、F、B在同一直线上,AC=BF,AE=BD,EF=CD.求证:∠AFE=∠BCD.
如图,A、C、F、B在同一直线上,AC=BF,AE=BD,EF=CD.求证:∠AFE=∠BCD.