题目内容
11.(1)解方程:x2-3x-4=0(2)解不等式组:$\left\{\begin{array}{l}{x-1>2}\\{x-3≤1+\frac{1}{2}x}\end{array}\right.$.
分析 (1)因式分解法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集..
解答 解:(1)∵(x+1)(x-4)=0,
∴(x+1)(x-4)=0,
则x+1=0或x-4=0,
解得:x=-1或x=4;
(2)解不等式x-1>2,得:x>3,
解不等式x-3≤1+$\frac{1}{2}$x,得:x≤8,
∴不等式组的解集为3<x≤8.
点评 本题考查的是解一元二次方程和解一元一次不等式组,正确求出每一个不等式解集是基础,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
1.有一个两位数$\overrightarrow{ab}$,互换两位数的数字顺序,得到两位数$\overrightarrow{ba}$,若这两个两位数和等于99,则所有满足条件的原两位数的和是396.
2.若$\sqrt{x}$+$\sqrt{\frac{1}{x}}$=$\sqrt{6}$,x≥1,则$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=( )
| A. | ±2 | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
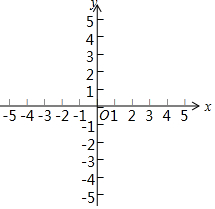 在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{a-2b-c=-4}\end{array}\right.$.
在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{a-2b-c=-4}\end{array}\right.$.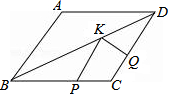 如图,菱形ABCD中,AB=3,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\frac{3\sqrt{3}}{2}$.
如图,菱形ABCD中,AB=3,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\frac{3\sqrt{3}}{2}$. 如图,在△ABC中,AD⊥BC于点D,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于点F,下列结论:①△ADE≌△BCE;②BD+DF=AD;③CE⊥DE;④S△BDE=S△ACE,其中正确的有①②③④(填写正确的番号)
如图,在△ABC中,AD⊥BC于点D,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于点F,下列结论:①△ADE≌△BCE;②BD+DF=AD;③CE⊥DE;④S△BDE=S△ACE,其中正确的有①②③④(填写正确的番号)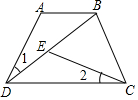 如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC,
如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC,