题目内容
12.阅读下列材料,解决问题:在处理分数和分式问题时,有时由于分子比分母大,或者分子的次数高于分母的次数,在实际运算时往往难度比较大,这时我们可以考虑逆用分数(分式)的加减法,将假分数(分式)拆分成一个整数(或整式)与一个真分数的和(或差)的形式,通过对简单式的分析来解决问题,我们称为分离整数法,此法在处理分式或整除问题时颇为有效,现举例说明.
材料1:将分式$\frac{{x}^{2}-x+3}{x+1}$拆分成一个整式与一个分式(分子为整数)的和的形式.
解:$\frac{{x}^{2}-x+3}{x+1}$=$\frac{x(x+1)-2(x+1)+5}{x+1}$=$\frac{x(x+1)}{x+1}$-$\frac{2(x+1)}{x+1}$+$\frac{5}{x+1}$=x-2+$\frac{5}{x+1}$
这样,分式$\frac{{x}^{2}-x+3}{x+1}$就拆分成一个整式x-2与一个分式$\frac{5}{x+1}$的和的形式.
材料2:已知一个能被11整除的个位与百位相同的三位整数100x+10y+x,且1≤x≤4,求y与x的函数关系式.
解:∵$\frac{101x+10y}{11}$=$\frac{99x+11y+2x-y}{11}$=9x+y+$\frac{2x-y}{11}$,
又∵1≤x≤4,0≤y≤9,∴-7≤2x-y≤8,还要使$\frac{2x-y}{11}$为整数,
∴2x-y=0,即y=2x.
(1)将分式$\frac{{x}^{2}+6x-3}{x-1}$拆分成一个整式与一个分子为整数的分式的和的形式,则结果为x+7+$\frac{4}{x-1}$;
(2)已知整数x使分式$\frac{2{x}^{2}+5x-20}{x-3}$的值为整数,则满足条件的整数x=2或4或-10或16;
(3)已知一个六位整数$\overline{20xy17}$能被33整除,求满足条件的x,y的值.
分析 (1)将分子x2+6x-3化为(x-1)(x+7)+4,依据题意可得;
(2)将分子2x2+5x-20化为(x-3)(2x+11)+13,依题意可得;
(3)由题意得出$\frac{200017+1000x+100y}{33}$=6061+30x+3y+$\frac{10x+y+4}{33}$,即可知10x+y+4为33的倍数,据此可得.
解答 解:(1)$\frac{{x}^{2}+6x-3}{x-1}$=$\frac{{x}^{2}-x+7x-7+4}{x-1}$
=$\frac{x(x-1)+7(x-1)+4}{x-1}$
=$\frac{(x-1)(x+7)+4}{x-1}$
=x+7+$\frac{4}{x-1}$,
故答案为:x+7+$\frac{4}{x-1}$;
(2)$\frac{2{x}^{2}+5x-20}{x-3}$=$\frac{2{x}^{2}-6x+11x-33+13}{x-3}$
=$\frac{2x(x-3)+11(x-3)+13}{x-3}$
=$\frac{(x-3)(2x+11)+13}{x-3}$
=2x+11+$\frac{13}{x-3}$,
∵分式$\frac{2{x}^{2}+5x-20}{x-3}$的值为整数,
∴$\frac{13}{x-3}$是整数,
∴x-3=±1或x-3=±13,
解得:x=2或4或-10或16,
故答案为:2或4或-10或16;
(3)$\frac{200017+1000x+100y}{33}$=$\frac{6061×33+4+30x•33+10x+3y•33+y}{33}$
=$\frac{33(6061+30x+3y)+10x+y+4}{33}$
=6061+30x+3y+$\frac{10x+y+4}{33}$,
∵整数$\overline{20xy17}$能被33整除,
∴$\frac{10x+y+4}{33}$为整数,即10x+y+4=33k,(k为整数),
当k=1时,x=2、y=9符合题意;
当k=2时,x=6、y=2符合题意;
当k=3时,x=9、y=5符合题意.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的计算方法.

 走进文言文系列答案
走进文言文系列答案| A. | ±2 | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
 如图,在△ABC中,AD⊥BC于点D,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于点F,下列结论:①△ADE≌△BCE;②BD+DF=AD;③CE⊥DE;④S△BDE=S△ACE,其中正确的有①②③④(填写正确的番号)
如图,在△ABC中,AD⊥BC于点D,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于点F,下列结论:①△ADE≌△BCE;②BD+DF=AD;③CE⊥DE;④S△BDE=S△ACE,其中正确的有①②③④(填写正确的番号)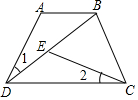 如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC,
如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC,