题目内容
6.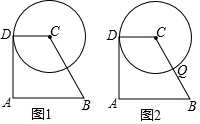 如图1,四边形ABCD中,AB∥CD,AB=2CD=2$\sqrt{3}$,AD=3,⊙C与AD相切于点D,P是线段AB上一动点,以点P为圆心,PB长为半径作⊙P.
如图1,四边形ABCD中,AB∥CD,AB=2CD=2$\sqrt{3}$,AD=3,⊙C与AD相切于点D,P是线段AB上一动点,以点P为圆心,PB长为半径作⊙P.(1)当⊙P经过点D时,求AP的长;
(2)如图2,设BC与⊙C交于点Q,将⊙C沿某直线l折叠,使点D恰好落在点Q,当⊙P与直线l相切时,求⊙P的半径;
(3)在(2)的条件下,在直线AB上的其它位置是否还存在相应的点P,使得⊙P与直线l相切?若存在,直接写出此时⊙P的半径;若不存在,请说明理由.
分析 (1)如图1所示:连接DP,然后在△APD中,依据勾股定理可求得PD的长,从而求得⊙P的半径;
(2)连接AC,过点P作PH⊥AC,AC与圆P的切点为H,连接HP,由∠DCA=∠ACB=60°可得到直线l与直线AC重合,设PB=a,然后在△AHP中,依据特殊锐角三角形函数值列出关于a的方程,从而可求得⊙P的半径;
(3)存在.当P在AB的延长线上时,设⊙P与AC相切于点H,设PB=PH=b.在Rt△APH中,根据cosP=$\frac{PH}{AP}$=$\frac{\sqrt{3}}{2}$,可得$\frac{b}{2\sqrt{3}+b}$=$\frac{\sqrt{3}}{2}$,推出b=12+6$\sqrt{3}$;
解答 解:(1)设AP=x,
当⊙P经过点D时,(如图1所示),则PB=PD=2 $\sqrt{3}$-x,
∵∠DOP=90°,
∴AD2+AP2=PD2,
即32+x2=(2 $\sqrt{3}$-x)2,
解得:x=$\frac{\sqrt{3}}{4}$,
∴PA=$\frac{\sqrt{3}}{4}$;
(2)连接AC,(如图2所示),
∵AB=2CD=2$\sqrt{3}$,
∴CD=$\sqrt{3}$,∵AD=3,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=2 $\sqrt{3}$,tan∠DAC=$\frac{\sqrt{3}}{3}$,
∴∠DAC=30°,
∴∠CAB=60°,
∴△ACB是等边三角形,
∴∠ACB=∠ACD=60°,
∴直线l经过点O,
过PH⊥AC于H,则∠APH=30°,设BP=PH=a,则AP=2 $\sqrt{3}$-a,
∴$\frac{PH}{PA}$=cos30°,
即 $\frac{a}{2\sqrt{3}-a}$=$\frac{\sqrt{3}}{2}$,
解得:a=12-6 $\sqrt{3}$,
当⊙P与直线l相切时,求⊙P的半径为12-6 $\sqrt{3}$.
(3)存在.当P在AB的延长线上时,设⊙P与AC相切于点H,设PB=PH=b.
在Rt△APH中,cosP=$\frac{PH}{AP}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{b}{2\sqrt{3}+b}$=$\frac{\sqrt{3}}{2}$,
∴b=12+6$\sqrt{3}$,
∴⊙P的半径为12+6$\sqrt{3}$
点评 本题主要考查的是圆的综合应用,解答本题主要应用了圆的性质、切线的性质、等边三角形的性质和判定、特殊锐角三角函数值等知识,解题的关键是依据勾股定理和特殊锐角三角函数值,列出关于a、b的方程.

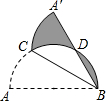 如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.
如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.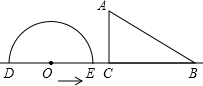 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.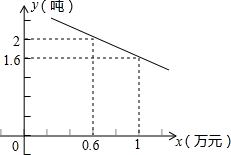 伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.
伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.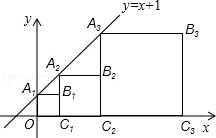 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为(2n-1,2n-1).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为(2n-1,2n-1). 如图,边长为2的菱形ABCD的两个顶点A、B分别在x轴、y轴上运动,C、D在第一象限,∠BCD=120°,则OD的最大值是( )
如图,边长为2的菱形ABCD的两个顶点A、B分别在x轴、y轴上运动,C、D在第一象限,∠BCD=120°,则OD的最大值是( )