题目内容
9.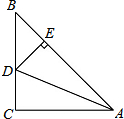 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是5cm,则AB的长为5cm.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是5cm,则AB的长为5cm.
分析 根据角平分线上的点到角的两边距离相等可得CD=DE,再判断出△BDE是等腰直角三角形,设BE=xcm,然后根据△BDE的周长列方程求出x的值,再分别求解即可.
解答 解:∵∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,
∴CD=DE,
∵AC=BC,
∴∠B=45°,
∴△BDE是等腰直角三角形,
设BE=xcm,则CD=DE=xcm,BD=$\sqrt{2}$xcm,
∵△BDE的周长是5cm,
∴x+x+$\sqrt{2}$x=5,
解得x=5-$\frac{5\sqrt{2}}{2}$,
∴AC=BC=x+$\sqrt{2}$x=5-$\frac{5\sqrt{2}}{2}$+$\sqrt{2}$(5-$\frac{5\sqrt{2}}{2}$)=$\frac{5\sqrt{2}}{2}$,
AB=$\sqrt{2}$AC=$\sqrt{2}$×$\frac{5\sqrt{2}}{2}$=5cm.
故答案为:5cm.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形周长的定义,等腰直角三角形的判定与性质,根据三角形的周长列出方程是解题的关键.

练习册系列答案
相关题目
20.下列对$\sqrt{11}$的大小估计正确的是( )
| A. | 在1和2之间 | B. | 在2和3之间 | C. | 在3和4之间 | D. | 在4和5之间 |
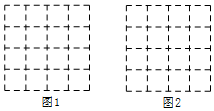 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.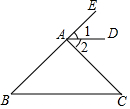 如图,已知AD∥BC,∠1=∠2,问∠B和∠C相等吗?为什么?
如图,已知AD∥BC,∠1=∠2,问∠B和∠C相等吗?为什么?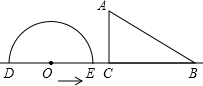 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.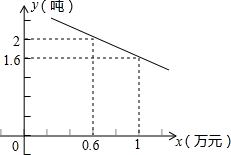 伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示.
伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销量y(吨)(纵坐标)与每吨的销售价x万元(横坐标)之间的函数关系如图所示. 如图,边长为2的菱形ABCD的两个顶点A、B分别在x轴、y轴上运动,C、D在第一象限,∠BCD=120°,则OD的最大值是( )
如图,边长为2的菱形ABCD的两个顶点A、B分别在x轴、y轴上运动,C、D在第一象限,∠BCD=120°,则OD的最大值是( )