题目内容
20.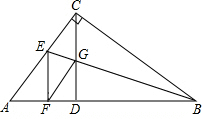 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.
分析 由△BFG≌△BCG,得到BD=BC,再证△BFE≌△BCE,即可得到结论.
解答 证明;∵∠ACB=90°,CD⊥AB,
∴∠A=∠BCD,
∵GF∥AB,
∴∠GFD=∠A,
∴∠BCD=∠GFD,
在△BFG与△BCG中,$\left\{\begin{array}{l}{∠BCD=∠GFD}\\{∠CBE=∠FBE}\\{BG=BG}\end{array}\right.$,
∴△BFG≌△BCG,
∴BF=BC,
在△CBE与△BCG中,$\left\{\begin{array}{l}{BC=BF}\\{∠CBE=∠FBE}\\{BE=BE}\end{array}\right.$,
∴△CBE≌△BFE,
∴∠EFB=∠ECB=90°,
∴EF⊥AB.
点评 本题考查了直角三角形的性质,平行线的性质,全等三角形的判定与性质,证明三角形全等是解题的关键.

练习册系列答案
相关题目
7.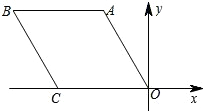 如图,菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
如图,菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
 如图,菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )
如图,菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=60°,则B点的坐标是( )| A. | (3,$\sqrt{3}$) | B. | (1,$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-3,$\sqrt{3}$) |
15.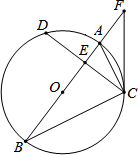 如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
(1)求证:CF是⊙O的切线.
(2)若AC=4,CE=2AE,求⊙O的半径.
 如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.(1)求证:CF是⊙O的切线.
(2)若AC=4,CE=2AE,求⊙O的半径.
5.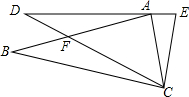 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )| A. | DC | B. | BC | C. | AB | D. | AE+AC |
10.刻画一组数据波动大小的统计量是( )
| A. | 平均数 | B. | 方差 | C. | 众数 | D. | 中位数 |
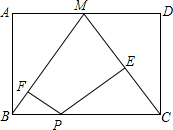 如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点,PE⊥CM,PF⊥BM,垂足分别E,F.
如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点,PE⊥CM,PF⊥BM,垂足分别E,F.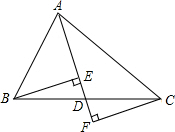 如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.
如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF. 已知:如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=$\frac{1}{2}$BP.
已知:如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=$\frac{1}{2}$BP.