题目内容
9. 已知:如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=$\frac{1}{2}$BP.
已知:如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=$\frac{1}{2}$BP.
分析 根据全等三角形的判定方法SAS可证得△BEC≌△ADB,根据各角的关系及三角形内角、外角和定理可证得∠BPQ=60°,即可得结论.
解答 解:AE=CD,AC=BC,
∴EC=BD;
∵△ABC为等边三角形,
∴∠C=∠ABC=60°,AB=BC,
在△BEC与△ADB中,
$\left\{\begin{array}{l}{EC=DB}\\{∠C=∠ABC}\\{AB=BC}\end{array}\right.$
∴△BEC≌△ADB(SAS),
∴∠EBC=∠BAD;
∵∠ABE+∠EBC=60°,
∴∠ABE+∠BAD=60°,
∵∠BPQ是△ABP外角,
∴∠ABP+∠BAP=60°=∠BPQ,
又∵BQ⊥AD,
∴∠PBQ=30°,
∴PQ=$\frac{1}{2}$BP.
点评 本题主要考查了全等三角形的判定和性质,涉及到等边三角形、直角三角形、三角形内角及外角和定理等知识点,是一道难度中等的综合题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17. 某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
(1)直接写出a、b、c的值,并补全条形统计图.
(2)这次抽样调查的数据中,中位数在哪个分数段.
(3)已知本次竞赛中有5人获得满分,其中有三名女职工,两名男职工.请用树状图或列表的方法求“从这五位满分获得者中随机抽取两人刚好是一男一女”的概率.
 某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图| 成绩(分) | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 |
| 频数(人) | 20 | 32 | a | b | c |
| 频率 | 0.08 | 0.20 | 0.36 |
(2)这次抽样调查的数据中,中位数在哪个分数段.
(3)已知本次竞赛中有5人获得满分,其中有三名女职工,两名男职工.请用树状图或列表的方法求“从这五位满分获得者中随机抽取两人刚好是一男一女”的概率.
1.下列命题中是真命题的是( )
| A. | 阴天会下雨是必然事件 | |
| B. | 若关于x的一元二次方程kx2-2x-1=0有实数根,则k≥-1 | |
| C. | 在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k | |
| D. | 多边形的外角和等于360° |
18.李明家一周内每天的用电量是(单位:kwh):10,8,9,10,12,7,6,这组数据的中位数和众数分别是( )
| A. | 7和10 | B. | 10和12 | C. | 9和10 | D. | 10和10 |
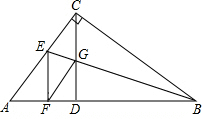 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.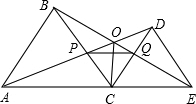 如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.
如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.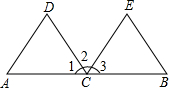 如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.