题目内容
7.先化简:$\frac{a+1}{a-3}$-$\frac{a-3}{a+2}$÷$\frac{a^2-6a+9}{a^2-4}$,然后a在3,2,-2和-3四个数中任选一个合适的数代入求值.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把a=-3代入计算即可求出值.
解答 解:原式=$\frac{a+1}{a-3}$-$\frac{a-3}{a+2}$•$\frac{(a+2)(a-2)}{(a-3)^{2}}$=$\frac{a+1}{a-3}$-$\frac{a-2}{a-3}$=$\frac{3}{a-3}$,
当a=-3时,原式=-$\frac{1}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.不等式1≤$\frac{x-2}{3}$<5的解集是( )
| A. | 3≤x≤15 | B. | 5≤x<13 | C. | 5≤x<17 | D. | -3≤x<15 |
15.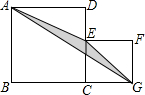 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )| A. | a2-b2 | B. | $\frac{2}{3}({a}^{2}-{b}^{2})$ | C. | $\frac{1}{2}{b}^{2}$ | D. | $\frac{1}{2}{a}^{2}$ |
19.若关于x的一元二次方程x2-(a+5)x+8a=0的两个实数根分别为2和b,则ab=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
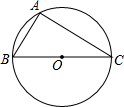 如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.
如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.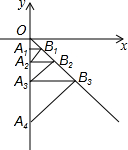 如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,在过点A2作y轴的垂线,交直线y=-x于点B2 …则点B2的坐标为($\frac{2}{3}$,-$\frac{2}{3}$).
如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,在过点A2作y轴的垂线,交直线y=-x于点B2 …则点B2的坐标为($\frac{2}{3}$,-$\frac{2}{3}$).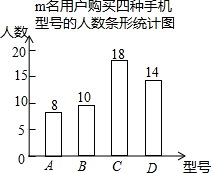 为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题:
为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题: 完成证明,说明理由.
完成证明,说明理由.