题目内容
19.若关于x的一元二次方程x2-(a+5)x+8a=0的两个实数根分别为2和b,则ab=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据根与系数的关系得到$\left\{\begin{array}{l}{2+b=a+5}\\{2b=8a}\end{array}\right.$,通过解该方程组可以求得a、b的值.
解答 解:∵关于x的一元二次方程x2-(a+5)x+8a=0的两个实数根分别是2、b,
∴由韦达定理,得$\left\{\begin{array}{l}{2+b=a+5}\\{2b=8a}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=1}\\{b=4}\end{array}\right.$.
∴ab=1×4=4.
故选:B.
点评 本题考查了根与系数的关系.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
14.据统计2015年1月至2016年1月,聊城市东昌湖、光岳楼、山陕会馆、宋代铁塔、古运河、姜提乐园、凤凰苑科技观光园、梦幻乐园等各景区共接待游客约518000人,这个数可用科学记数法表示为( )
| A. | 0.518×104 | B. | 5.18×105 | C. | 51.8×104 | D. | 518×103 |
11.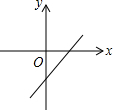 一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )
一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )
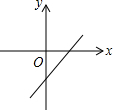 一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )
一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )| A. | k>0,b>2 | B. | k>0,b<2 | C. | k<0,b>2 | D. | k<0,b<2 |
8.九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
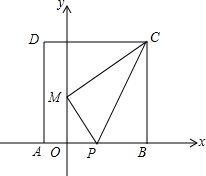 将正方形ABCD放置在如图所示的直角坐标系中,点B的坐标为(8,0),点P在边AB的中点.连结CP,将△BCP沿PC折叠,使点B落在y轴的M点处,且点M的纵坐标为4.若点Q是x轴正半轴上一个运动的点,连结MQ、CQ,则△CMQ周长的最小值为10+2$\sqrt{65}$.
将正方形ABCD放置在如图所示的直角坐标系中,点B的坐标为(8,0),点P在边AB的中点.连结CP,将△BCP沿PC折叠,使点B落在y轴的M点处,且点M的纵坐标为4.若点Q是x轴正半轴上一个运动的点,连结MQ、CQ,则△CMQ周长的最小值为10+2$\sqrt{65}$.