题目内容
17. 完成证明,说明理由.
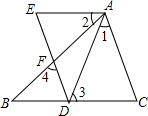
完成证明,说明理由.已知:如图,点D在BC边上,DE、AB交于点F,AC∥DE,∠1=∠2,∠3=∠4.
求证:AE∥BC.
证明:∵AC∥DE(已知),
∴∠4=∠FAC(两直线平行,同位角相等 )
∵∠3=∠4(已知),
∴∠3=∠FAC(等量代换 )
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD(等式的性质)
即∠FAC=∠EAD,
∴∠3=∠EAD.
∴AE∥BC(内错角相等,两直线平行 )
分析 首先根据平行线的性质可得∠4=∠FAC,然后可得∠3=∠FAC,再证明∠FAC=∠EAD,从而可得∠3=∠EAD,根据平行线的判定可得AE∥BC.
解答 解:∵AC∥DE(已知),
∴∠4=∠FAC(两直线平行,同位角相等)
∵∠3=∠4(已知),
∴∠3=∠FAC(等量代换)
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD(等式的性质)
即∠FAC=∠EAD,
∴∠3=∠EAD.
∴AE∥BC(内错角相等,两直线平行 ).
故答案为:∠FAC;两直线平行,同位角相等;∠FAC;等量代换;等式的性质;∠EAD;内错角相等,两直线平行.
点评 此题主要考查了平行线的判定和性质,关键是掌握两直线平行,同位角相等;内错角相等,两直线平行.

练习册系列答案
相关题目
8.九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
2.若式子$\sqrt{2x+1}$在实数范围内有意义,则x的取值范围是( )
| A. | x$≤-\frac{1}{2}$ | B. | x$≥-\frac{1}{2}$ | C. | x$<-\frac{1}{2}$ | D. | x$>-\frac{1}{2}$ |
7.某居民小区共有300户家庭,有关部门对该小区的自来水管网系统进行改进,为此需了解该小区自来水用水量的情况,该部门通过随机抽样,调查了其中20户家庭,统计了这20户家庭的月用水量,见如表:
(1)这个问题中样本是其中20户家庭自来水用水量,样本容量是20;
(2)计算这20户家庭的平均月用水量;
(3)根据上述数据,估计该小区300户家庭的月总用水量.
| 月用水量(m3) | 4 | 6 | 7 | 12 | 14 | 15 |
| 户数 | 2 | 4 | 6 | 2 | 2 | 4 |
(2)计算这20户家庭的平均月用水量;
(3)根据上述数据,估计该小区300户家庭的月总用水量.