题目内容
13.求下列二项式的积:(1)(x+4)(x+3)(x-2);
(2)(x-1)(x+3)(x-5)(x+7);
(3)(x+2y)(x-3y)(x-5y)
分析 多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.
解答 解:(1)(x+4)(x+3)(x-2)
=(x2+7x+12)(x-2)
=x3+5x2-2x-24;
(2)(x-1)(x+3)(x-5)(x+7)
=(x2+2x-3)(x2+2x-35)
=(x2+2x)2-38(x2+2x)+105
=x4+4x3+4x2-38x2-76x+105
=x4+4x3-34x2-76x+105;
(3)(x+2y)(x-3y)(x-5y)
=(x2-xy-6y2)(x-5y)
=x3-6x2y-xy2+30y3.
点评 此题考查了多项式与多项式相乘,运用法则时应注意以下两点:①相乘时,按一定的顺序进行,必须做到不重不漏;②多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.

练习册系列答案
相关题目
3.下列说法错误的是( )
| A. | 三角形中至少有两个锐角 | |
| B. | 两条边及一角对应相等的三角形全等 | |
| C. | 两个角及一边对应相等的三角形全等 | |
| D. | 三角形的外角大于不相邻的内角 |
 如图,两条交叉的公路上分别有A、B两个车站,要在这两条公路之间修一个储运仓库,使它到两条公路的距离相等,且又要到两个车站的距离相等,请你在图中画出这个储运仓库P的位置.
如图,两条交叉的公路上分别有A、B两个车站,要在这两条公路之间修一个储运仓库,使它到两条公路的距离相等,且又要到两个车站的距离相等,请你在图中画出这个储运仓库P的位置. 已知:如图,△ABC内接于⊙O,AB=AC,D为BC上任意一点,连接AD,BD,求证:∠ABD=∠AEB.
已知:如图,△ABC内接于⊙O,AB=AC,D为BC上任意一点,连接AD,BD,求证:∠ABD=∠AEB.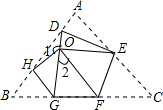 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=142°,则∠2的度数为38°.
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=142°,则∠2的度数为38°.