题目内容
19. 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PD⊥AB,垂足为D,射线DP交$\widehat{AC}$于点E,交过点C的切线于点F.
如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PD⊥AB,垂足为D,射线DP交$\widehat{AC}$于点E,交过点C的切线于点F.(1)求证:FC=FP;
(2)若∠CAB=30°,当E是$\widehat{AC}$的中点时,判断以A,O,C,E为顶点的四边形是什么特殊四边形,并说明理由.
分析 (1)连接OC,根据切线的性质得出OC⊥CF以及∠OAC=∠OCA得∠FCP=∠FPC,可证得结论;
(2)由∠CAB=30°易得△AOE、△EOC均是等边三角形,可得AE=AO=OC=CE,易得以A,O,C,E为顶点的四边形是菱形.
解答 (1)证明:连接OC
∵CF是⊙O的切线,
∴OC⊥CF,
∴∠FCA+∠ACO=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∵PD⊥AB,
∴∠PAD+∠APD=90°,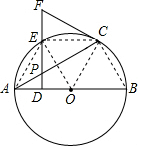
而∠APD=∠CPF,
∴∠PAD+∠CPF=90°,
∴∠FCP=∠FPC,
∴FC=FP;
(2)解:以A,O,C,E为顶点的四边形是菱形,
理由如下:
∵∠CAB=30°,
∴∠ABC=60°,从而∠AOC=120°,
∵E是$\widehat{AC}$的中点,
∴∠AOE=∠EOC=60°,
∴△AOE、△EOC均是等边三角形,
∴AE=AO=OC=CE,
∴四边形AOCE是菱形.
点评 本题主要考查了切线的性质、圆周角定理和等边三角形的判定等,作出恰当的辅助线利用切线的性质是解答此题的关键.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | 2πx2的系数是2 | B. | -xy2的次数为2 | C. | -5x2+x=-4x3 | D. | 3x2-x2=2x2 |
13. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | AC=BD | C. | ∠ACB=∠DBC | D. | AB=DC |
8.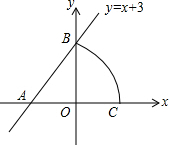 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为( )| A. | (3$\sqrt{2}$-3,0) | B. | (3$\sqrt{2}$,0) | C. | (0,3$\sqrt{2}$-3) | D. | (3,0) |
 如图:线段AD=8cm,线段AC=BD=6cm,E、F分别是线段AB、CD的中点,EF的长是6cm.
如图:线段AD=8cm,线段AC=BD=6cm,E、F分别是线段AB、CD的中点,EF的长是6cm.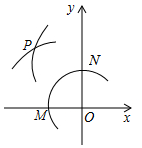 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )