题目内容
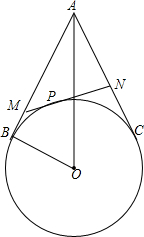 已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.
已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.考点:切线长定理
专题:
分析:根据切线的性质,可得出OB⊥AB,再根据勾股定理得出AB的长,根据切线长定理得出三角形的周长为定值,即可得出这个定值.
解答:解:∵AB,AC分别与⊙O相切,
∴OB⊥AB,
∵AO=d,BO=r,
∴AB=
=
,
∵MN切圆O于点P,
∴MP=MB,NP=NC,
∴△AMN的周长=AM+AN+MN=AM+PM+PN+AN=AM+BM+AN+PN=AB+AC=2AB=2
,
∴△AMN的周长是一个定值,这个定值为2
.
∴OB⊥AB,
∵AO=d,BO=r,
∴AB=
| AO2-OB2 |
| d2-r2 |
∵MN切圆O于点P,
∴MP=MB,NP=NC,
∴△AMN的周长=AM+AN+MN=AM+PM+PN+AN=AM+BM+AN+PN=AB+AC=2AB=2
| d2-r2 |
∴△AMN的周长是一个定值,这个定值为2
| d2-r2 |
点评:本题考查了切线长定理,即经过圆外一点作圆的两条切线,切线长相等且此点与圆心的连线平分两切线的夹角,考查了数形结合的数学思想,是一道中档题.理解过点D和点E分别作圆的两条切线是解本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
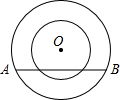 如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )
如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )| A、8≤AB≤10 |
| B、8<AB<10 |
| C、8<AB≤10 |
| D、6≤AB≤10 |
下面四个数中,最小的数是( )
| A、-2 | ||
| B、0 | ||
| C、0.2 | ||
D、-
|
 【问题情境】
【问题情境】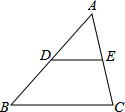 如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为
如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为  如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF 如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,你知道BE与AC有什么位置关系吗,请说明理由.
如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,你知道BE与AC有什么位置关系吗,请说明理由. 如图,在⊙O中,AC、BD为直径.求证:AB∥CD.
如图,在⊙O中,AC、BD为直径.求证:AB∥CD.