题目内容
 如图所示为一矩形木框,四周为宽度相同的木条,那么这个矩形框的里、外两个矩形是相似形码?假设木框长为30cm,宽为20cm,木条的宽度为2cm,试加以验证.
如图所示为一矩形木框,四周为宽度相同的木条,那么这个矩形框的里、外两个矩形是相似形码?假设木框长为30cm,宽为20cm,木条的宽度为2cm,试加以验证.考点:相似多边形的性质
专题:
分析:先求出外面矩形的长与宽,然后求出里、外两个矩形的长与宽的比,然后根据相似多边形的对应边成比例判断即可.
解答:解:外面矩形的长为30+2=32cm,
宽为20+2=22cm,
里外两个矩形的长的比=
=
,
宽的比=
=
,
∵
≠
,
∴这个矩形框的里、外两个矩形不是相似形.
宽为20+2=22cm,
里外两个矩形的长的比=
| 30 |
| 32 |
| 15 |
| 16 |
宽的比=
| 20 |
| 22 |
| 10 |
| 11 |
∵
| 15 |
| 16 |
| 10 |
| 11 |
∴这个矩形框的里、外两个矩形不是相似形.
点评:本题考查了相似多边形的性质,主要利用了相似多边形的对应边成比例,求出长的比与宽的比是解题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、若|a|=|b|,则a=b |
| B、若ac=bc,则a=b |
| C、若线段AC=BC,则点C是线段AB的中点 |
| D、过n边形的一个顶点有(n-3)条对角线 |
下面四个数中,最小的数是( )
| A、-2 | ||
| B、0 | ||
| C、0.2 | ||
D、-
|
 如图是一个几何体的俯视图,则该几何体可能是( )
如图是一个几何体的俯视图,则该几何体可能是( )A、 |
B、 |
C、 |
D、 |
已知平行四边形ABCD,下列判断正确的是( )
| A、若∠A=90°,则四边形ABCD是矩形 |
| B、AC=BD |
| C、AB=CD,则ABCD是菱形 |
| D、若AC丄BD,则四边形ABCD为正方形 |
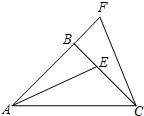 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF 如图,圆O是三角形ABC的内切圆,求证:AB+CF=AC+BF.
如图,圆O是三角形ABC的内切圆,求证:AB+CF=AC+BF.