题目内容
16.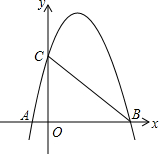 如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).
如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).(1)求此抛物线的解析式;
(2)抛物线在第一象限内是否存在点P,过P作PM⊥x轴于M,使得以A,P,M为顶点的三角形与△BOC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
分析 (1)将三点代入即可求出此抛物线的解析式;
(2)由于BO=OC,∠BOC=90°,所以△BOC是等腰直角三角形,设出点P的坐标,使AM=PM,据此即可得解.
解答 解:(1)设抛物线的解析式为:y=ax2+bx+c,
将点A(-1,0),点B(3,0)和点C(0,3)代入可得:$\left\{\begin{array}{l}{c=3}\\{a-b+c=0}\\{9a+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$.
∴此抛物线的解析式为:y=-x2+2x+3;
(2)存在,如图,过点P作PM⊥x轴,垂足为M,连接AP,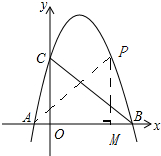
∵BO=OC=3,∠BOC=90°,
∴△BOC是等腰直角三角形,
设点P(m,-m2+2m+3)(0<m<3),
则:AM=m+1,PM=-m2+2m+3,
若Rt△BOC∽Rt△AMP,则:AM=PM,
∴m+1=-m2+2m+3,
解得:m=2,或m=-1,
又∵0<m<3,
∴m=2,
∴P(2,3).
点评 本题主要考查了用待定系数法求抛物线的解析式,以及二次函数与三角形相似的综合问题,仔细分析△BOC的结构特点是解题的关键,有比较强的综合性,要注意认真总结.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
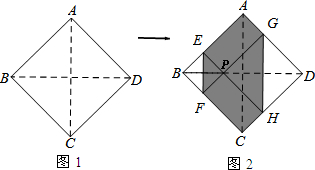
8.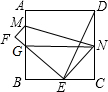 如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
 如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
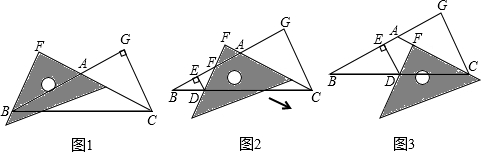
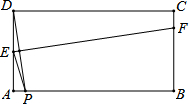 如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.
如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.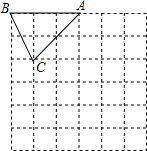 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1.