题目内容
11.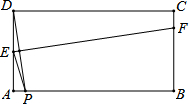 如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.
如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.
分析 由要使四边形EPFD为菱形,则需DE=EP=FP=DF,可得当点E与点A重合时,AP最小;当点P与点B重合时,AP最大,继而求得四边形EPFD为菱形的AP的取值范围,进而得到S的取值范围.
解答 解:∵要使四边形EPFD为菱形,则需DE=EP=FP=DF,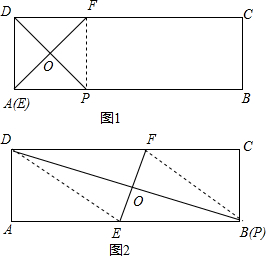
∴如图1:当点E与点A重合时,AP=AD=1,此时AP最小;
此时,S=AP2=1.
如图2:当点P与B重合时,AP=AB=2,此时AP最大;
此时,设AE=x,则EP=DE=2-x,根据勾股定理得:12+x2=(2-x)2,
解得:x=$\frac{3}{4}$,
∴EP=$\frac{5}{4}$,
∴S=1×$\frac{5}{4}$=$\frac{5}{4}$.
∴四边形EPFD为菱形时,S的取值范围:1≤S≤$\frac{5}{4}$.
故答案为:1≤S≤$\frac{5}{4}$.
点评 此题考查了菱形的判定与性质、折叠的性质、矩形的性质以及面积的计算.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.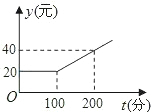 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
(1)通话时间为多少时,两家公司的收费是相同的?
(2)李女士想买一部手机,如果她的月通话时间不超过100分钟,她选择哪家通讯公司更合算?如果她的月通话时间超过100分钟,又将如何选择?
 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
(2)李女士想买一部手机,如果她的月通话时间不超过100分钟,她选择哪家通讯公司更合算?如果她的月通话时间超过100分钟,又将如何选择?
3.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….例如:点A1的坐标为(3,1),则点A2的坐标为(0,4),…;若点A1的坐标为(a,b),则点A2015的坐标为( )
| A. | (-b+1,a+1) | B. | (-a,-b+2) | C. | (b-1,-a+1) | D. | (a,b) |
20.下列计算正确的是( )
| A. | a4+a4=a8 | B. | (a3)4=a7 | ||
| C. | 12a6b4÷3a2b-2=4a4b2 | D. | (-a3b)2=a6b2 |
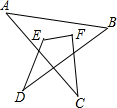 ∠A+∠B+∠C+∠D+∠E+∠F的度数=360°.
∠A+∠B+∠C+∠D+∠E+∠F的度数=360°.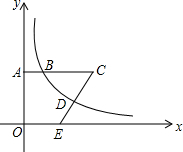 如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.
如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.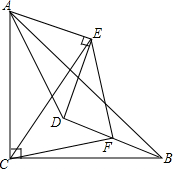 如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.
如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.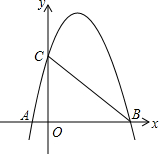 如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).
如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).