Question

5．已知，正方形ABCD的边长为4，点E是对角线BD延长线上一点，AE=BD．将△ABE绕点A顺时针旋转α度（0°＜α＜360°）得到△AB′E′，点B、E的对应点分别为B′、E′．
（1）如图1，当α=30°时，求证：B′C=DE；
（2）连接B′E、DE′，当B′E=DE′时，请用图2求α的值；
（3）如图3，点P为AB的中点，点Q为线段B′E′上任意一点，试探究，在此旋转过程中，线段PQ长度的取值范围为2$\sqrt{2}$-2≤PQ≤4$\sqrt{2}$+2．

Answer 1

分析 （1）先由正方形的性质得到直角三角形AOE，再经过简单计算求出角，判断出△ADE≌△AB′C即可；
（2）先判断出△AEB′≌△AE′D，再根据旋转角和图形，判断出∠BAB′=∠DAB′即可；
（3）先判断出点Q的位置，PQ最小时和最大时的位置，进行计算即可．

解答 解：（1）如图1，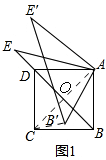

连接AC，B′C，
∵四边形ABCD是正方形，
∴AB=AD，AC⊥BD，AC=BD=2OA，∠CAB=ADB=45°，
∵AE=BD，
∴AC=AE=2OA，
在Rt△AOE中，∠AOE=90°，AE=2OA，
∴∠E=30°，
∴∠DAE=∠ADB-∠E=45°-30°=15°，
由旋转有，AD=AB=AB′∠BAB′=30°，
∴∠DAE=15°，
在△ADE和△AB′C中，$\left\{\begin{array}{l}{AD=AB′}\\{∠DAE=∠CAB′}\\{AE=AC}\end{array}\right.$，
∴△ADE≌△AB′C，
∴DE=B′C，
（2）如图2，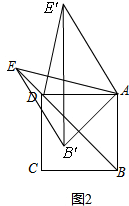

由旋转得，AB′=AB=AD，AE′=AE，
在△AEB′和△AE′D中，
$\left\{\begin{array}{l}{AE=AE′}\\{AD=AB′}\\{DB′=DE′}\end{array}\right.$，
∴△AEB′≌△AE′D，
∴∠DAE′=∠EAB′，
∴∠EAE′=∠DAB′，
由旋转得，∠EAE′=∠BAB′，
∴∠BAB′=∠DAB′，
∵∠BAB′+∠DAB′=90°，
∴α=∠BAB′=45°，或α=360°-90°-45°=225°；

（3）如图3，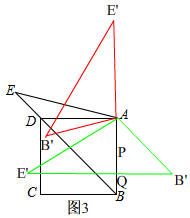

∵正方形ABCD的边长为4，
∴$\frac{1}{2}$BD=2$\sqrt{2}$，
在旋转过程中，△ABE在旋转到边B'E'⊥AB于Q，此时PQ最小，PQ=AQ-AP=$\frac{1}{2}$BD-AP=2$\sqrt{2}$-2
在旋转过程中，△ABE在旋转到点E在BA的延长线时，点Q和点E'重合，∴AE'=AE=4$\sqrt{2}$，
∴PE'=AE'+AP=4$\sqrt{2}$+2，
故答案为2$\sqrt{2}$-2≤PQ≤4$\sqrt{2}$+2．

点评 此题是四边形综合题，主要考查了正方形的性质，旋转的性质，全等三角形的判定和性质，直角三角形的判定，解本题的关键是判断出△AOE是直角三角形．