题目内容
如图,在△ABC中,AC=BC,D为底边AB上一动点(不与A、B重合),AH⊥BC于点H,DE⊥AC于点E,DF⊥BC于点F.
(1)试求AH、DE、DF的数量关系,并证明你的结论;
(2)若点D在AB延长线上,其他条件不变,那么上面的结论还存在吗?说明你的理由.
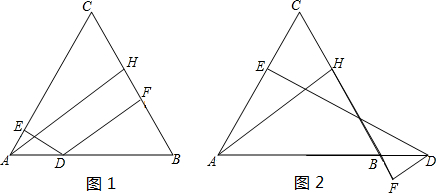
(1)试求AH、DE、DF的数量关系,并证明你的结论;
(2)若点D在AB延长线上,其他条件不变,那么上面的结论还存在吗?说明你的理由.

考点:等腰三角形的性质,三角形的面积
专题:
分析:(1)连接CD,可知S△ADC+S△BCD=S△ABC,可找到DE、DF、AH之间的关系;
(2)连接CD,可知S△ADC-S△BCD=S△ABC,从而可找到DE、DF、AH之间的关系.
(2)连接CD,可知S△ADC-S△BCD=S△ABC,从而可找到DE、DF、AH之间的关系.
解答: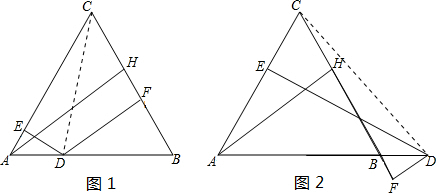 解:(1)连接CD,如图1,
解:(1)连接CD,如图1,
∵AH⊥BC,DE⊥AC,DF⊥BC,
∴S△ADC=
AC•DE,S△BCD=
BC•DF,S△ABC=
BC•AH,
∵S△ADC+S△BCD=S△ABC,
∴
AC•DE+
BC•DF=
BC•AH,
即AC•DE+BC•DF=BC•AH,
∵AC=BC,
∴DE+DF=AH;
(2)不存在,其关系为DE-DF=AH,理由如下:
连接CD,如图2,
同理可得S△ADC=
AC•DE,S△BCD=
BC•DF,S△ABC=
BC•AH,
∵S△ADC-S△BCD=S△ABC,
∴∴
AC•DE-
BC•DF=
BC•AH,
即AC•DE-BC•DF=BC•AH,
∵AC=BC,
∴DE-DF=AH.
 解:(1)连接CD,如图1,
解:(1)连接CD,如图1,∵AH⊥BC,DE⊥AC,DF⊥BC,
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ADC+S△BCD=S△ABC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即AC•DE+BC•DF=BC•AH,
∵AC=BC,
∴DE+DF=AH;
(2)不存在,其关系为DE-DF=AH,理由如下:
连接CD,如图2,
同理可得S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ADC-S△BCD=S△ABC,
∴∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即AC•DE-BC•DF=BC•AH,
∵AC=BC,
∴DE-DF=AH.
点评:本题主要考查等腰三角形的性质,在解题时利用等积法找到线段之间的关系是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
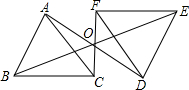 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )| A、点A与点D是对应点 |
| B、BO=EO |
| C、∠ACB=∠FDE |
| D、AB∥DE |
 如图,某隧道的截面是一个半径为4米的半圆,一辆载有大型货物的卡车宽4米,高3.6米,这辆车能通过该隧道吗?
如图,某隧道的截面是一个半径为4米的半圆,一辆载有大型货物的卡车宽4米,高3.6米,这辆车能通过该隧道吗?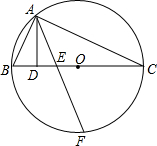 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是