题目内容
 已知:如图,在⊙O中,弦AB=CD,那么∠AOC和∠BOD相等吗?请说明理由.
已知:如图,在⊙O中,弦AB=CD,那么∠AOC和∠BOD相等吗?请说明理由.考点:圆心角、弧、弦的关系
专题:常规题型
分析:根据在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等由AB=CD得到∠AOB=∠COD,然后都减去∠BOC即可得到∠AOC=∠BOD.
解答:解:∠AOC和∠BOD相等.利用如下:
∵AB=CD,
∴∠AOB=∠COD,
∴∠AOB-∠COB=∠COD-∠COB,
即∠AOC=∠BOD.
∵AB=CD,
∴∠AOB=∠COD,
∴∠AOB-∠COB=∠COD-∠COB,
即∠AOC=∠BOD.
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 如图E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添加下列一个条件,仍不能判断出△ABC≌△DEF的是( )
如图E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添加下列一个条件,仍不能判断出△ABC≌△DEF的是( )| A、DF∥AC |
| B、AB=DE |
| C、AB∥DE |
| D、∠E=∠ABC |
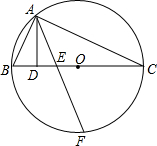 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是