题目内容
 已知:如图,AB是⊙O的直径,直线CD交⊙O于C、D两点,过A、B两点分别作AE⊥CD、BF⊥CD,垂足为点E、F,求证:CE=DF.
已知:如图,AB是⊙O的直径,直线CD交⊙O于C、D两点,过A、B两点分别作AE⊥CD、BF⊥CD,垂足为点E、F,求证:CE=DF.考点:垂径定理
专题:证明题
分析:作OH⊥CD于H,根据垂径定理得CH=DH,由于BF⊥CD,则OH∥BF,根据平行线分线段成比例定理得HE=HF,则CH-EH=HD-HF,易得CE=DF.
解答:证明:作 OH⊥CD于H,
OH⊥CD于H,
则CH=DH,
∵BF⊥CD,
∴OH∥BF,
而OA=OB,
∴HE=HF,
∴CH-EH=HD-HF,
即CE=DF.
 OH⊥CD于H,
OH⊥CD于H,则CH=DH,
∵BF⊥CD,
∴OH∥BF,
而OA=OB,
∴HE=HF,
∴CH-EH=HD-HF,
即CE=DF.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
 如图,某隧道的截面是一个半径为4米的半圆,一辆载有大型货物的卡车宽4米,高3.6米,这辆车能通过该隧道吗?
如图,某隧道的截面是一个半径为4米的半圆,一辆载有大型货物的卡车宽4米,高3.6米,这辆车能通过该隧道吗?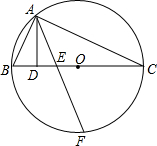 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
 如图,在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE,求证:AE=BE+GE.
如图,在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE,求证:AE=BE+GE.