题目内容
1.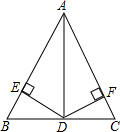 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;
(2)若AB=8,∠B=60°,则CF的长为2.
分析 (1)由角平分线的性质可求得DE=DF,则可证明Rt△BDE≌Rt△CDF,可求得∠B=∠C,可证得AB=AC;
(2)由(1)的结论,结合条件可知△ABC为等边三角形,则可求得CD,在Rt△CDF中可求得CF=$\frac{1}{2}$CD,可求得答案.
解答 (1)证明:
∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
在Rt△BDE和Rt△CDF中
$\left\{\begin{array}{l}{DE=DF}\\{BD=CD}\end{array}\right.$
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C,
∴AB=AC;
(2)解:
∵AB=AC,且∠B=60°,
∴△ABC为等边三角形,
∴BC=AB=8,∠C=∠B=60°,
∵BD=CD,
∴CD=$\frac{1}{2}$BC=4,
在Rt△CDF中,可求得∠CDF=30°,
∴CF=$\frac{1}{2}$CD=2,
故答案为:2.
点评 本题主要考查全等三角形的判定和性质及等边三角形的性质和判定,在(1)中证得∠B=∠C是解题的关键,在(2)中求得CD的长是解题的关键.

练习册系列答案
相关题目
6. 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )| A. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| B. | 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 | |
| C. | 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上 | |
| D. | 用2、3、4三个数字随机排成一个三位数,排出的数是偶数 |
 已知:如图,点A、B、C在同一直线上,AC=BD,AE∥CF,且AE=CF.求证:∠E=∠F.
已知:如图,点A、B、C在同一直线上,AC=BD,AE∥CF,且AE=CF.求证:∠E=∠F. 如图,有一块四边形形状的铁皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.
如图,有一块四边形形状的铁皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.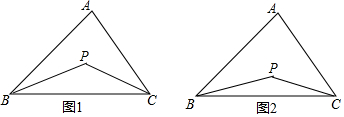 【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗? 如图所示,直线AD和BC被直线AB所截,∠1和∠2是同位角;∠4、∠FAC与∠2也是同位角.
如图所示,直线AD和BC被直线AB所截,∠1和∠2是同位角;∠4、∠FAC与∠2也是同位角.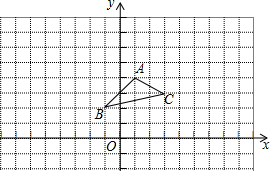 如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(-1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.
如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(-1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.