题目内容
11. 已知:如图,点A、B、C在同一直线上,AC=BD,AE∥CF,且AE=CF.求证:∠E=∠F.
已知:如图,点A、B、C在同一直线上,AC=BD,AE∥CF,且AE=CF.求证:∠E=∠F.
分析 根据题意利用全等三角形的判定,边角边可以证明△EAB≌△FCD,即可证明∠E=∠F.
解答 解:∵点A、B、C在同一直线上,AC=BD,
∴AC=AB+BC,BD=CD+BC,
∴AB=CD,
又∵AE∥CF,且AE=CF,
∴∠A=∠FCD,
∴$\left\{\begin{array}{l}{EA=FC}\\{∠A=∠FCD}\\{AB=BC}\end{array}\right.$,
∴△EAB≌△FCD(SAS),
∴∠E=∠F.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.下列各式计算正确的是( )
| A. | 6$\sqrt{3}$-2$\sqrt{3}$=4 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{3}$=6$\sqrt{6}$ | D. | 6$\sqrt{2}$÷2$\sqrt{2}$=3$\sqrt{2}$ |
6.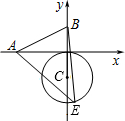 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )| A. | 2+$\frac{\sqrt{5}}{2}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 3+$\frac{\sqrt{3}}{2}$ | D. | 4+$\frac{\sqrt{3}}{2}$ |
20.下列条件中,不能判定三角形全等的是( )
| A. | 三条边对应相等 | B. | 两边和其中一角对应相等 | ||
| C. | 两边和夹角对应相等 | D. | 两角和它们的夹边对应相等 |
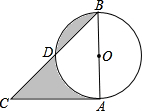 如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图形阴影部分的面积为1.
如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图形阴影部分的面积为1.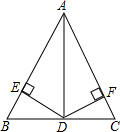 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.