题目内容
9. 如图,有一块四边形形状的铁皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.
如图,有一块四边形形状的铁皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.求:(1)∠BCD的度数;
(2)该圆锥的底面半径.
分析 (1)由已知条件可得∠DBC=30°,所以∠DBC=60°,则△CDB为等边三角形,进而求出∠C的度数;
(2)利用弧长公式可以求出弧BD的长,即圆锥底面圆的周长,从而求出圆的半径.
解答 解:(1)∵∠ABC=90°,AB=2AD,
∴sin∠ABD=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴∠ABD=30°,
∵∠ADB=90°,
∴∠DBC=90°-30°=60°,
∵BC=CD=6,
∴△CBD是等边三角形,
∴∠BCD=60°;
(2)∵${l}_{\widehat{BD}}$=$\frac{60π×12}{180}$=2π,
∴2π=2πr,
∴r=1.
点评 本题考查了直角三角形的性质、等边三角形的判定和等边三角形的性质以及考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
20.下列条件中,不能判定三角形全等的是( )
| A. | 三条边对应相等 | B. | 两边和其中一角对应相等 | ||
| C. | 两边和夹角对应相等 | D. | 两角和它们的夹边对应相等 |
19.据统计,2009年在国际金融危机的强烈冲击下,我国国内生产总值约为30 067 000 000 000元,仍比上年增长9.0%.30 067 000 000 000元用科学记数法表示为(保留三位有效数字)( )
| A. | 3.0037×1013元 | B. | 3.00×1013元 | C. | 30.1×1012元 | D. | 3.01×1013元 |
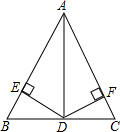 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.