题目内容
13. 已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.(1)求证:AM平分∠DAB.
(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.
分析 (1)过M作ME⊥AD于E,根据角平分线性质求出ME=MC=MB,再根据角平分线性质求出即可;
(2)根据平行线性质求出∠BAD+∠DC=180°,求出∠MAD+∠MDA=90°,即可求出答案.
解答 (1)证明:过M作ME⊥AD于E,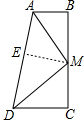
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME,
∵M为BC的中点,
∴BM=MC=ME,
∵∠B=90°,ME⊥AD,
∴AM平分∠DAB;
(2)AM⊥DM,
证明:∵AB∥DC,
∴∠BAD+∠ADC=180°,
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=$\frac{1}{2}$∠BAD,∠MDA=$\frac{1}{2}$∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∴AM⊥DM.
点评 本题考查了梯形的性质,平行线的性质,角平分线性质的应用,主要考查学生综合运用性质进行推理的能力,难度适中.

练习册系列答案
相关题目
3.直角三角形的两条边长分别是5和12,则斜边上的中线长是( )
| A. | 6 | B. | 6.5 | C. | 6或 6.5 | D. | 6或 2.5 |
 如图所示,已知数 a,b,c 在数轴上对应点的位置:化简|a-b|+|b-c|得2b-a-c.
如图所示,已知数 a,b,c 在数轴上对应点的位置:化简|a-b|+|b-c|得2b-a-c. 如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).
如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).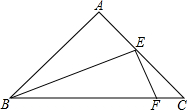 如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.
如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.