题目内容
5. 如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).
如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).(1)求该反比例函数的关系式;
(2)设PC⊥y轴于点C,点A关于y轴对称点为A′,求△ABC的周长和sin∠BA′C的值.
分析 (1)设反比例函数的解析式为y=$\frac{k}{x}$,把点P坐标代入即可解决问题.
(2)如图,连接AC、BA′、CA′,作CH⊥BA′于H.由sin∠BA′C=$\frac{CH}{CA′}$可知,求出CH、CA′即可解决问题.
解答 解:(1)设反比例函数的解析式为y=$\frac{k}{x}$,
∵反比例函数经过点P(2,1),
∴k=2,
∴y=$\frac{2}{x}$.
(2)如图,连接AC、BA′、CA′,作CH⊥BA′于H.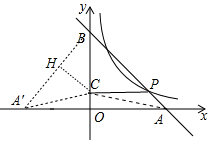
直对于线y=-x+3,令x=0得y=3,令y=0得x=3,
∴A(3,0),B(0,3),
∵PC⊥OB,P(2,1),
∴OC=1,OA=OB=OA′=3,BC=OB-OC=2,
∴S△ABC=$\frac{1}{2}$•BC•OA=$\frac{1}{2}$×2×3=3,
在Rt△OCA′中,CA′=$\sqrt{OA{′}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
在Rt△BOA′中,BA′=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵sin∠CBH=$\frac{CH}{BC}$=$\frac{OA′}{BA′}$=$\frac{3}{3\sqrt{2}}$,
∴CH=$\sqrt{2}$,
∴sin∠BA′C=$\frac{CH}{CA′}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查反比例函数综合题、一次函数的应用、锐角三角函数,勾股定理、三角形的面积公式等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.甲打电话给乙:“你在哪儿啊?”在下面乙的回话中,甲能确定乙位置的是( )
| A. | 我和你相距500米 | |
| B. | 我在你北偏东30°的方向500米处 | |
| C. | 我在你北偏东30°的方向 | |
| D. | 你向北走433米,然后转90°再走250米 |
20.已知:x2-5xy+4y2=0,且xy≠0,则x:y=( )
| A. | 1或4 | B. | 1或$\frac{1}{4}$ | C. | -1或-4 | D. | -1或-$\frac{1}{4}$ |
1.以下问题,最适合做全面调查的是( )
| A. | 对中央台“新闻联播”栏目收视率的调查 | |
| B. | 了解七(3)班同学订购校服的尺码情况 | |
| C. | 对一个社区每天丢弃塑料袋数量的调查 | |
| D. | 了解全省中学生每周进行体育锻炼时间 |

 已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.