题目内容
8.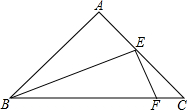 如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.
如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.
分析 过C作CD⊥CE与EF的延长线交于D,构成直角三角形可证出Rt△ABE∽Rt△CED,然后证出其面积.
解答 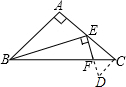 解:如图,过C作CD⊥CE与EF的延长线交于D.
解:如图,过C作CD⊥CE与EF的延长线交于D.
因为∠ABE+∠AEB=90°,∠CED+∠AEB=90°,所以∠ABE=∠CED.
于是Rt△ABE∽Rt△CED,
所以$\frac{{S}_{△CDE}}{{S}_{△EAB}}$=($\frac{CE}{AB}$)2=$\frac{1}{4}$.
又∠ECF=∠DCF=45°,所以CF是∠DCE的平分线,点F到CE和CD的距离相等,
所以$\frac{{S}_{△CEF}}{{S}_{△CDF}}$=$\frac{CE}{CD}$=2.
所以S△CEF=$\frac{2}{3}$S△CDE=$\frac{2}{3}$×$\frac{1}{4}$S△ABE=$\frac{2}{3}$×$\frac{1}{4}$×$\frac{1}{2}$S△ABC=$\frac{1}{24}$.
故答案是:$\frac{1}{24}$.
点评 本题考查了相似三角形的判定与性质,关键是作出辅助线,然后构成直角三角形,用相似三角形的性质求面积.

练习册系列答案
相关题目
20.已知:x2-5xy+4y2=0,且xy≠0,则x:y=( )
| A. | 1或4 | B. | 1或$\frac{1}{4}$ | C. | -1或-4 | D. | -1或-$\frac{1}{4}$ |
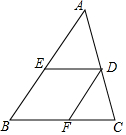 如图,在△ABC中,AB=20,BC=12,D是AC上一点,过点D作DE∥BC交AB于E,作DF∥AB交BC于F,设四边形BEDF为菱形.
如图,在△ABC中,AB=20,BC=12,D是AC上一点,过点D作DE∥BC交AB于E,作DF∥AB交BC于F,设四边形BEDF为菱形. 已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
 如图,∠DCE=∠EBC=∠A=90°且DC=EC,猜测AB、AC、AD三者的数量关系,并说明理由.
如图,∠DCE=∠EBC=∠A=90°且DC=EC,猜测AB、AC、AD三者的数量关系,并说明理由. 如图,正方体纸盒的棱长为4,点M、N分别在CD、HE上,CM=$\frac{1}{4}$CD,点N是HE的中点,将纸盒展开,若HC与NM的延长线交于点Q,则tan∠QNH=4.
如图,正方体纸盒的棱长为4,点M、N分别在CD、HE上,CM=$\frac{1}{4}$CD,点N是HE的中点,将纸盒展开,若HC与NM的延长线交于点Q,则tan∠QNH=4.