题目内容
17.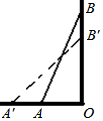 如图,梯子AB靠在墙上,梯子底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
如图,梯子AB靠在墙上,梯子底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )| A. | 小于1 m | B. | 大于1 m | C. | 等于1 m | D. | 小于或等于1 m |
分析 由题意可知OA=2,OB=7,先利用勾股定理求出AB,梯子移动过程中长短不变,所以AB=A′B′,又由题意可知OA′=3,利用勾股定理分别求OB′长,把其相减得解.
解答 解:在直角三角形AOB中,
∵OA=2,OB=7
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{7}^{2}}$=$\sqrt{53}$.
由题意可知AB=A′B′=$\sqrt{53}$,
又∵OA′=3,根据勾股定理得:OB′=$\sqrt{A′B{′}^{2}-OA{′}^{2}}$=$\sqrt{53-9}$=$\sqrt{44}$,
∴BB′=7-$\sqrt{44}$<1.
故选A.
点评 本题考查了勾股定理的应用,属于基础题,解答本题的关键是掌握勾股定理的表达式.

练习册系列答案
相关题目
8.下列语句中,是真命题的是( )
| A. | 若ab>0,则a>0,b>0 | B. | 若ab=0,则a=0或b=0 | ||
| C. | 内错角相等 | D. | 相等的角是对顶角 |
12.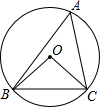 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )| A. | 22.5° | B. | 35° | C. | 45° | D. | 67.5° |
2.下列四个数中,最小的是( )
| A. | -3 | B. | -2 | C. | 3 | D. | 5 |
6. 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
 如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.
如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.